Предмет: Математика,
автор: Askezis
Решите пожалуйста Срочно надо
Приложения:
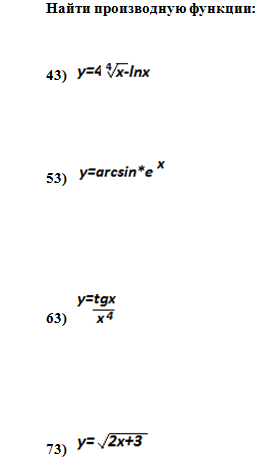
Ответы
Автор ответа:
0
43) дифференцируем 4x^(1/4)−ln(x) почленно:Производная произведения константы на функцию есть произведение этой константы на производную данной функции.Производная ln(x) является 1/x.Таким образом, в результате: −1/xПроизводная произведения константы на функцию есть произведение этой константы на производную данной функции.В силу правила, применим: x^(1/4) получим 1/4x^(3/4)Таким образом, в результате: 1/x^(3/4)В результате: −1/x+1/x^(3/4)
=exp(x)*asin(x) + exp(x) / sqrt(-x^2 + 1).
63) Применим правило производной частного:ddx(f(x)g(x))=1g2(x)(−f(x)ddxg(x)+g(x)ddxf(x))f(x)=tan(x) и g(x)=x⁴.Чтобы найти ddxf(x):Есть несколько способов вычислить эту производную.Один из способов: ddxtan(x)=1/cos²(x)Чтобы найти ddxg(x):В силу правила, применим: x⁴ получим 4x³Теперь применим правило производной деления:(1/x⁸)((x⁴/cos²(x))(sin²(x)+cos²(x))−4x³tan(x))Теперь упростим: (x−2sin(2x)) / (x⁵cos²(x)
1/(√(2x+3))
Ответ: −1/x+1/x^(3/4)
53) Результат вычисления производной от функции
f(x) = exp(x)*asin(x):
ℯ^(x) ⋅asin(x) +ℯ^(x) / ( (- x² + 1)^(1/2)) ==exp(x)*asin(x) + exp(x) / sqrt(-x^2 + 1).
63) Применим правило производной частного:ddx(f(x)g(x))=1g2(x)(−f(x)ddxg(x)+g(x)ddxf(x))f(x)=tan(x) и g(x)=x⁴.Чтобы найти ddxf(x):Есть несколько способов вычислить эту производную.Один из способов: ddxtan(x)=1/cos²(x)Чтобы найти ddxg(x):В силу правила, применим: x⁴ получим 4x³Теперь применим правило производной деления:(1/x⁸)((x⁴/cos²(x))(sin²(x)+cos²(x))−4x³tan(x))Теперь упростим: (x−2sin(2x)) / (x⁵cos²(x)
Ответ: (x−2sin(2x)) / (x⁵cos²(x))
73) Заменим u=2x+3.
В силу правила, применим: √u получим 1/2√u
Затем примените цепочку правил. Умножим на ddx(2x+3):дифференцируем 2x+3 почленно:Производная постоянной 3 равна нулю.Производная произведения константы на функцию есть произведение этой константы на производную данной функции.В силу правила, применим: x получим 1Таким образом, в результате: 2В результате последовательности правил:1/(√(2x+3))
Ответ: 1/(√2x+3))
Похожие вопросы
Предмет: История,
автор: Daft2
Предмет: Информатика,
автор: saradauchiha24
Предмет: Биология,
автор: ievlevandrey6
Предмет: Алгебра,
автор: AnastasiaLisa
Предмет: Химия,
автор: soronastya