Question

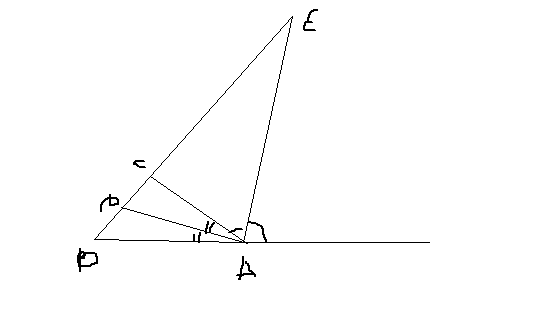
Из вершины A треугольника ABC проведены биссектрисы внутреннего и внешнего углов, пересекающие прямую BC в точках D и E соответственно. Определить отношение AB / AC , если BD / DE =3 / 5.

Answer 1

СОГЛАСНО ТЕОРЕМЕ О БИССЕКТРИСЕ ВНУТРЕННЕГО УГЛА, получаем отношение АВ/АС=ВД/ДС
согласно теореме о биссектрисе внешнего угла получаем отношение АВ/АС=ВЕ/СЕ
пусть ВД=3х, ДЕ=5х, ВЕ=8х, ДС=кх, СЕ=5х-кх тогда учитывая оба равенства и подстановку имеем
3х/кх=8х/5х-кх
3/к=8/5-к
15-3к=8к
к=15/11
АВ/АС=3/(15/11)=11/5