Question

Площадь прямоугольного треугольника равна 242*корень3/3. Один из острых углов равен 30. Найдите длину катета, прилежащего к этому углу

Answer 1

Дано:
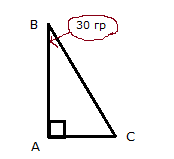
ABC-прямоугольный. Угол А=90 гр., Угол В=30 гр. $S= frac{242 sqrt{3} }{3}$. Найти АВ.

Решение:
$S= frac{1}{2}AB*AC; \ cosB= frac{AB}{BC};cos C= frac{AC}{BC};[tex][tex]AB=BCcosB; AC=BCcosC;[tex][tex]S= frac{1}{2}BC^2cos30^{0}cos60^{0}; \ 2S=BC^2 frac{ sqrt{3} }{2}*frac{1}{2}; \ frac{ sqrt{3} }{4}BC^2= frac{484 sqrt{3}}{3};$$BC= sqrt{ frac{484 sqrt{3}*4 }{3* sqrt{3} } }= frac{44}{ sqrt{3}}= frac{44 sqrt{3} }{3};$
$AB= frac{44 sqrt{3}}{3}* frac{ sqrt{3} }{2}=22.$
Ответ: AB=22.