Question

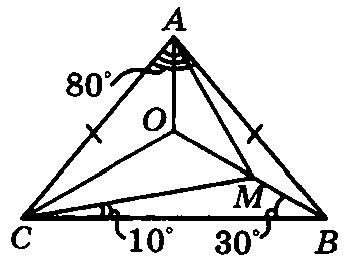
В равнобедренном треугольнике ABC с основанием BC угол при вершине A равен 80o. Внутри треугольника ABC взята точка M так, что MBC = 30o и MCB = 10o. Найдите величину угла AMC.

Answer 1

∠B = ∠C =(180°-80°) : 2 = 50°. AO - биссектриса угла А, где точка О - точка пересечения ВМ и АО. Имеем:

▲AOC = ▲AOB по первому признаку, отсюда ∠ACO =∠ABO = ∠ABC - ∠MBC= 20°. Тогда ∠AOB =∠AOC = 180° - ∠ABO - 1/2∠A = 120°

Поэтому ∠MOC = 360°- ∠AOC - ∠AOB = 120° , а ∠OCM = ∠ACB -∠OCA -∠MCB = 20°

Имеем: ▲ACO = ▲MCO (∠MOC =∠AOC, ∠OCM =∠OCA, OC - общая)

отсюда

АС = МС и ▲AМС - равнобедренный. Получаем:∠ACM =∠C -∠MCB=40°, ∠AMC= (180°-40°) : 2 = 70°

Ответ: ∠AMC = 70°

(смотрите рисунок ниже)

Answer 2

Верно. В архив.