Предмет: Алгебра,
автор: SkoobyLi
Решите неравенство. По какому правилу можно определить ОДЗ этого неравенства? Даю 28 баллов за объяснение.
Приложения:
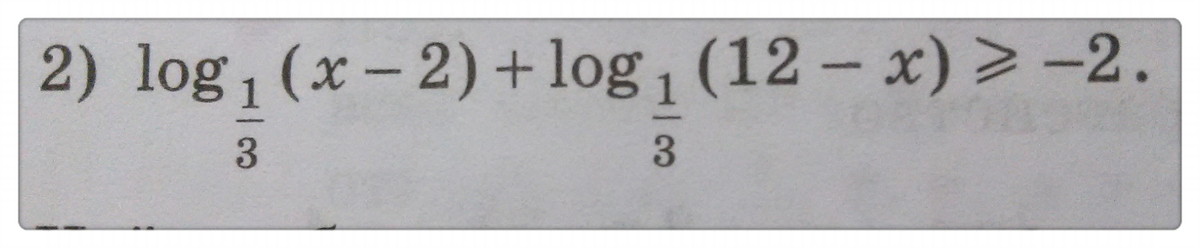
Ответы
Автор ответа:
0
log_(1/3) (x - 2) + log_(1/3) (12 - x) ≥ - 2
ОДЗ: x - 2 > 0, x > 2
12 - x > 0
- x > - 12
x < 12
х ∈ (2 ;12)
log_(1/3) (x - 2)*(12 - x) ≥ - 2
Так как 0 < 1/3 < 1, то знак неравенства меняется на противоположный
(x - 2)*(12 - x) ≤ 3²
12x - x² - 24 + 2x - 9 ≤ 0
- x² + 14x - 33 ≤ 0 умножаем на (-1), и снова знак неравенства меняется на противоположный
x² - 14x + 33 ≥ 0
По т. Виета находим корни уравнения:
x₁ = 11
x₂ = 3
+ - +
------------------------------------------------------>
3 11 x
x ∈ (- ≈ ; 3] [11 ; + ≈)
С учётом ОДЗ, получаем: ( 2 ; 3] [11;12)
Ответ: ( 2 ; 3] [11;12)
ОДЗ: x - 2 > 0, x > 2
12 - x > 0
- x > - 12
x < 12
х ∈ (2 ;12)
log_(1/3) (x - 2)*(12 - x) ≥ - 2
Так как 0 < 1/3 < 1, то знак неравенства меняется на противоположный
(x - 2)*(12 - x) ≤ 3²
12x - x² - 24 + 2x - 9 ≤ 0
- x² + 14x - 33 ≤ 0 умножаем на (-1), и снова знак неравенства меняется на противоположный
x² - 14x + 33 ≥ 0
По т. Виета находим корни уравнения:
x₁ = 11
x₂ = 3
+ - +
------------------------------------------------------>
3 11 x
x ∈ (- ≈ ; 3] [11 ; + ≈)
С учётом ОДЗ, получаем: ( 2 ; 3] [11;12)
Ответ: ( 2 ; 3] [11;12)
Похожие вопросы
Предмет: Математика,
автор: zavarkabs
Предмет: Геометрия,
автор: Аноним
Предмет: Қазақ тiлi,
автор: fatimaalim32
Предмет: Математика,
автор: lanushkaok
Предмет: Математика,
автор: oleghahlupin