Предмет: Алгебра,
автор: Аноним
Упростите выражение:

Источник: Крамор В.С. Повторяем и систематизируем школьный курс алгебры и начала анализа, М., 1990, с. 59
...если это не затруднительно, то чем подробнее было бы расписано решение, тем лучше, извиняюсь...
Ответы
Автор ответа:
0
Автор ответа:
0
...великолепно! огромное спасибо! (там 4 звёздочки я решению поставил, а не 5, так это по ошибке, случайно кликнулось, а исправить уже нельзя, но решение, конечно, на 5 звёзд, тут двух мнений быть не может(!))...
Автор ответа:
0
Спасибо.
Автор ответа:
0
----------------------------------------------
Приложения:
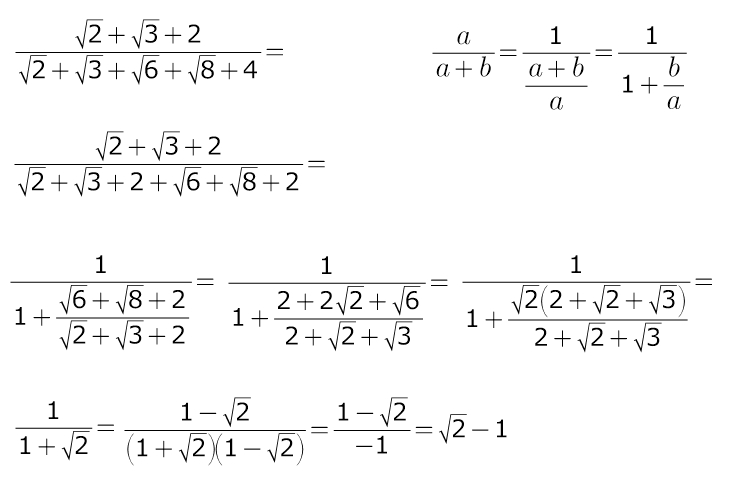
Автор ответа:
0
... а я по недоразумению пытался умножать на "корень из 2 + корень из 3 + 2"... вот, что больше всего мне нравится в этих решениях, так это когда двойка представляется как произведение двух корней из 2, додуматься до такого нюанса не хватило у меня остроты математического ума, и тут (особенно это рельефно показано в первом решении) возникает такой эффект-
Автор ответа:
0
[эффект] - кажется вот вроде бы решение: 2 = два корня из 2, значит один корень можно вынести за скобки, но ведь останеться не 2, а корень из 2, а в первой сумме к двум корням прибавляется просто двойка, казалось бы всё, тупик, ан нет: корень из 8 можно выразить как произведение корня из 2 (который выносится) на корень из 4, а корень из 4 как раз равняется 2 (!) и получается ровно такое же варажение, как и первое (корень из 2 + корень из 3 + 2), в этом для меня и заключается красота решения
Автор ответа:
0
[красота решения] (конечно, при хорошо развитых алгебраических навыках на это, вероятно, и не обращается внимание, но для меня это потребовала дополнительного "думанья"), и эта красота решения вполне достойна, на мой взгляд, называться искусством, и если бы существовал музей математических искусств, то этот пример с решением я бы в него поместил ...
Автор ответа:
0
...субъективно, на мой взгляд, первое решение, немного кажется "по-красивше" (возможно из-за отсутствия дроби в знаменателе), но во втором - показан очень полезный метод...
Автор ответа:
0
... то-есть, извиняюсь, метод, которым, я ещё не решал примеров, очень он пригодится, спасибо!
Похожие вопросы
Предмет: Английский язык,
автор: naza75
Предмет: Қазақ тiлi,
автор: karakatbazarbay
Предмет: Математика,
автор: Аноним
Предмет: Химия,
автор: elinalis
Предмет: Математика,
автор: Аноним