Предмет: Математика,
автор: Miracle97
помогите найти общий интеграл дифференциального уравнения. Ответ представить в виде . Найти интегральную кривую, проходящую через точку (1; 1).
Приложения:
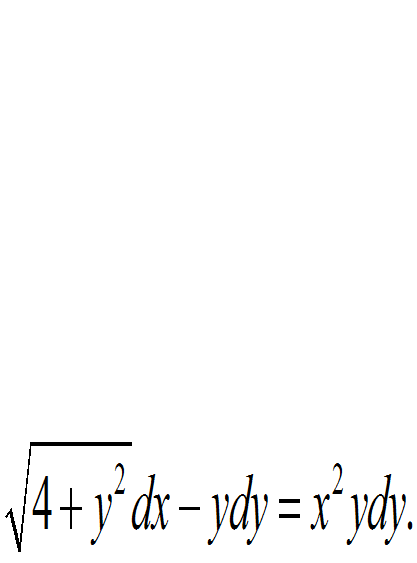
Ответы
Автор ответа:
0
Подставляем x = y = 1:
Похожие вопросы
Предмет: Химия,
автор: glafiratodorenko
Предмет: Русский язык,
автор: uu6731374
Предмет: Английский язык,
автор: kusarkuanyskerej
Предмет: Математика,
автор: aigulek85