Предмет: Алгебра,
автор: solopovakristi
Помогите решить, пожалуйста. Желательно с подробным решением!
Приложения:
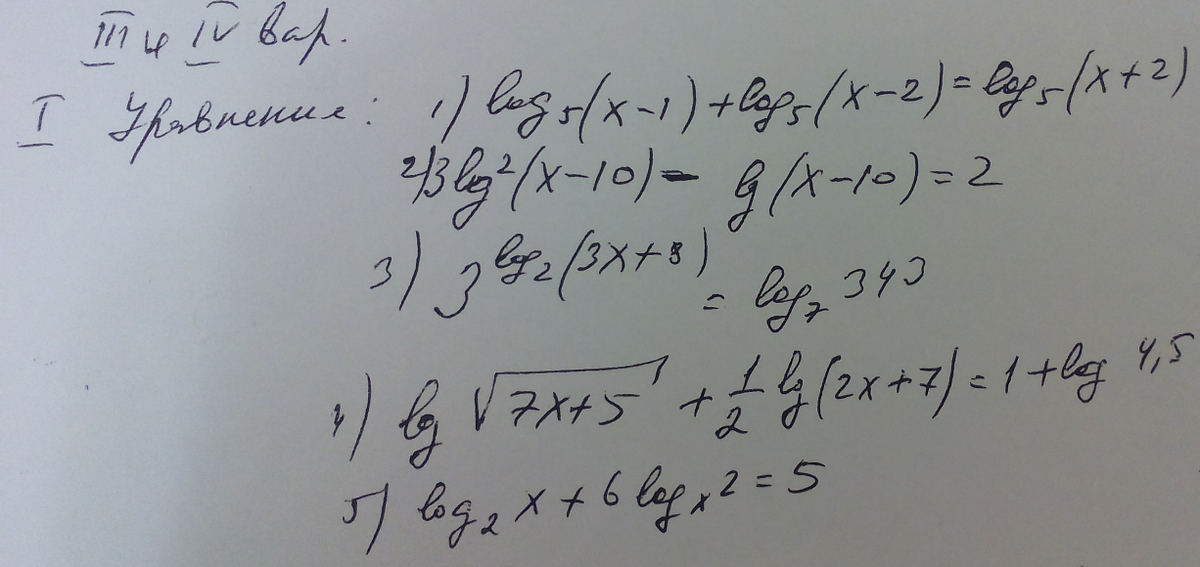
Ответы
Автор ответа:
0
1) В левой части уравнения сумма логарифмом равна логарифму произведения.По свойству логарифмов:
(х-1)(х-2)=х+2,
х^2-3x+2-x-2=0,
x^2-4x=0,
x(x-4)=0,
х=0 или х=4, корень х=4 удовлетворяет уравнение.
Ответ 4.
2) Сделаем замену: lg(x-10)=k,
3k^2-k-2=0,
k1=1,
k2=-2/3.
Произведем обратную замену:
lg(x-10)=1,
x-10=10,
x1=20.
lg(x-10)=-2/3.
x-10=10^(-2/3).
x-10=1/∛100,
x2=10+(1/∛100)
Ответ: 20; 10+(1/∛100).
3) Сразу отметим, что 343=7^3.
На основании этого можно утверждать, что правая часть уравнения равна 3.
Правая часть уравнения это степень с основанием 3, левая часть уравнения равно 3 в первой степени.
Можем приравнять показатели степеней
log_2(3x+8)=3.
3x+8=2^3,
3x+8=8,
3x=0,
x=0.
Ответ: 0.
4) lg√(7x+5)+0,5lg(2x+7)=1+lg4,5.
lg10=1,
0,5lg(2x+7)=lg√(2x+7).
Уравнение примет вид:
lg√(7x+5)+lg√(2x+7)=lg10+lg4,5.
Сумму логарифмов превратим в логарифм произведения в каждой части уравнения.
lg√(7x+5)(2x+7)=lg10·4,5;
√(7x+5)(2x+7)=45;
Возведем обе части уравнения в квадрат
(7х+5)(2х+7)=2025;
Раскроем скобки и приведем подобные
14х^2+59x-1990=0;
После решения квадратного уравнения получим корень, который удовлетворяет наше уравнение
х=10.
Ответ: 10.
5) log_2(x)+log_x(2)=5.
Приведем логарифмы к общему основанию
1/(log_x(2))+6log_x(2)=5,
Произведем замену
log_x(2)=k,
уравнение примет вид
(1/k) +6k=5,
6k^2-5k+1=0.
Решая квадратное уравнение получим два корня:
k1=1/2; k2=1/3.
Произведем обратную замену
log_x(2)=1/2; √x=2; x1=4.
log_x(2)=1/3; ∛x=2; x2=2^3=8.
Ответ: 4; 8.
(х-1)(х-2)=х+2,
х^2-3x+2-x-2=0,
x^2-4x=0,
x(x-4)=0,
х=0 или х=4, корень х=4 удовлетворяет уравнение.
Ответ 4.
2) Сделаем замену: lg(x-10)=k,
3k^2-k-2=0,
k1=1,
k2=-2/3.
Произведем обратную замену:
lg(x-10)=1,
x-10=10,
x1=20.
lg(x-10)=-2/3.
x-10=10^(-2/3).
x-10=1/∛100,
x2=10+(1/∛100)
Ответ: 20; 10+(1/∛100).
3) Сразу отметим, что 343=7^3.
На основании этого можно утверждать, что правая часть уравнения равна 3.
Правая часть уравнения это степень с основанием 3, левая часть уравнения равно 3 в первой степени.
Можем приравнять показатели степеней
log_2(3x+8)=3.
3x+8=2^3,
3x+8=8,
3x=0,
x=0.
Ответ: 0.
4) lg√(7x+5)+0,5lg(2x+7)=1+lg4,5.
lg10=1,
0,5lg(2x+7)=lg√(2x+7).
Уравнение примет вид:
lg√(7x+5)+lg√(2x+7)=lg10+lg4,5.
Сумму логарифмов превратим в логарифм произведения в каждой части уравнения.
lg√(7x+5)(2x+7)=lg10·4,5;
√(7x+5)(2x+7)=45;
Возведем обе части уравнения в квадрат
(7х+5)(2х+7)=2025;
Раскроем скобки и приведем подобные
14х^2+59x-1990=0;
После решения квадратного уравнения получим корень, который удовлетворяет наше уравнение
х=10.
Ответ: 10.
5) log_2(x)+log_x(2)=5.
Приведем логарифмы к общему основанию
1/(log_x(2))+6log_x(2)=5,
Произведем замену
log_x(2)=k,
уравнение примет вид
(1/k) +6k=5,
6k^2-5k+1=0.
Решая квадратное уравнение получим два корня:
k1=1/2; k2=1/3.
Произведем обратную замену
log_x(2)=1/2; √x=2; x1=4.
log_x(2)=1/3; ∛x=2; x2=2^3=8.
Ответ: 4; 8.
Похожие вопросы
Предмет: Литература,
автор: bkupehov1976
Предмет: Алгебра,
автор: bodikborikbodik
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Математика,
автор: Antoha92