Предмет: Алгебра,
автор: Seijurou
помогите решить логарифмическое неравенство
Приложения:
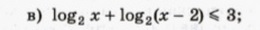
Ответы
Автор ответа:
0
Отметим ОДЗ:
x ∈ (3;+∞)
По т. Виете
Полученное решение отметим на рисунке
(3)___-____[4]___+____>
Ответ: x ∈ (3;4]
Похожие вопросы
Предмет: Қазақ тiлi,
автор: dilyabek0907
Предмет: Қазақ тiлi,
автор: lidados83
Предмет: Математика,
автор: inbalinadinara
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: slon210