Предмет: Алгебра,
автор: Аноним
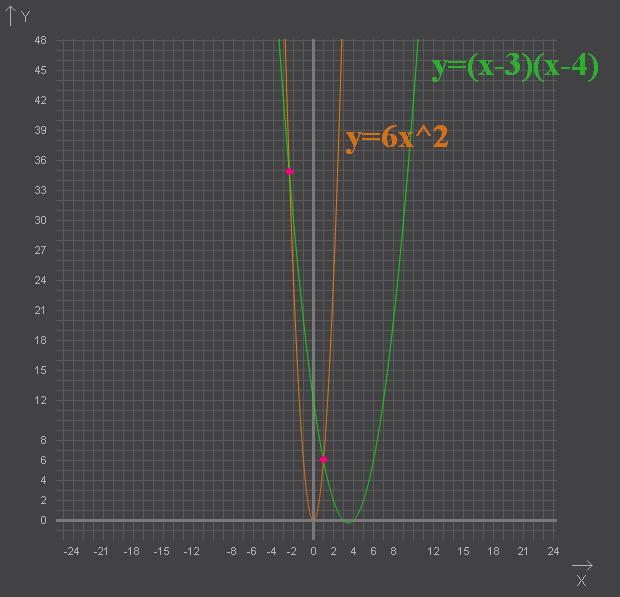
Найдите площадь фигуры, ограниченной параболами у=6x^{2} , у=(х-3)(х-4) и осью Ох
ПИШИТЕ ОЧЕНЬ ПОДРОБНО И С ЧЕРТЕЖОМ!
Ответы
Автор ответа:
0
Для начала находим абсциссы точек пересечения заданных графиков:


Ответ:
Ответ:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: batyrbatyrok
Предмет: Математика,
автор: dinaamangildina19
Предмет: Математика,
автор: verakazanceva
Предмет: Алгебра,
автор: PIROZHULKA
Предмет: Математика,
автор: mariapetrova76