Question

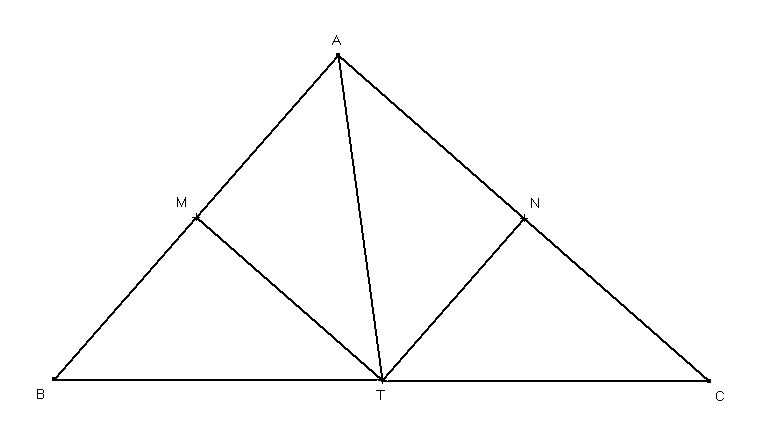
серединные перпендикуляры к сторонам ab и ac треугольника abc пересекаются в точке стороны bc. докажите что угол a= угол b + угол c

Answer 1

Пусть серединные перпендикуляры MT и NT к сторонам AB и AC соответственно пересекаются в точке T, принадлежащей стороне BC. Проведём отрезок AT и рассмотрим треугольник ABT. В этом треугольнике TM является одновременно медианой и высотой, поскольку TM - серединный перпендикуляр к стороне AB треугольника. Так как TM одновременно является медианой и высотой, треугольник ABT равнобедренный с основанием AB, тогда углы ABT и BAT равны. Аналогично, рассмотрим треугольник ACT, в нём TN является одновременно медианой и высотой, поскольку TN - серединный перпендикуляр к стороне AC треугольника. Значит, треугольник ACT равнобедренный с основанием AC и углы ACT и CAT равны. Тогда угол A=BAC равен BAT+TAC=ABT+ACT=B+C, что и требовалось доказать.