Предмет: Геометрия,
автор: shevchenko0501
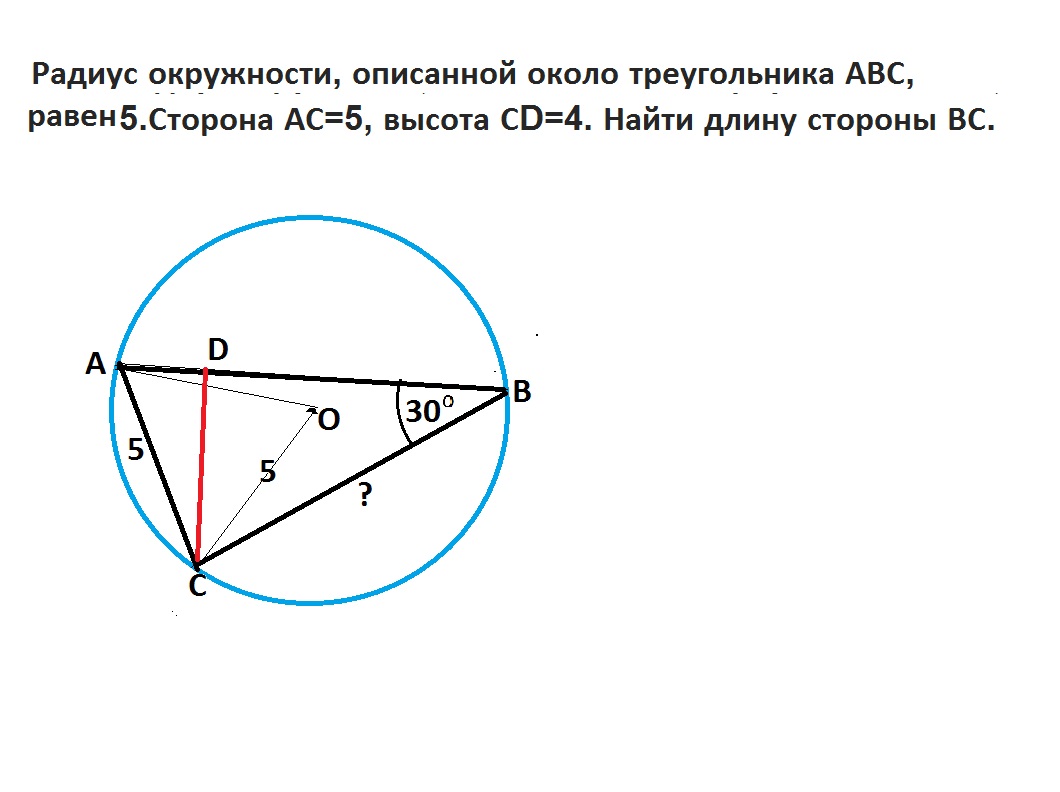
Радиус окружности, описанной около треугольника АВС, равен 5.Сторона АС=5, высота СD=4. Найти длину стороны ВС.
Ответы
Автор ответа:
0
По условию сторона АС вписанного треугольника АВС равна радиусу описанной вокруг него окружности.
Следовательно, эта сторона с радиусами окружности образует равносторонний треугольник и как хорда стягивает дугу 60°.
Где бы ни находилась на окружности вершина вписанного угла, опирающегося на хорду АС, этот угол будет равен половине центрального угла, опирающегося на ту же дугу, которую стягивает эта хорда.
Угол АВС равен половине центрального угла, т.е. 30°.
Высота СД противолежит этому углу, и потому гипотенуза СВ треугольника СВD вдвое больше СD
ВС=2*СD=2*4=8
или, иначе, СВ=СD:sin(60°) =4:0,5=8
Приложения:
Похожие вопросы
Предмет: Обществознание,
автор: tapcomrusdaw
Предмет: Алгебра,
автор: kirill4558
Предмет: Геометрия,
автор: baylii25
Предмет: Математика,
автор: nik5644
Предмет: Алгебра,
автор: Alenka345