Question

Центр окружности, описанной около трапеции, делит ее высоту в отношении 3:4. Найти основания трапеции, ели радиус равен 10, и ее средняя линия равна высоте.

Answer 1

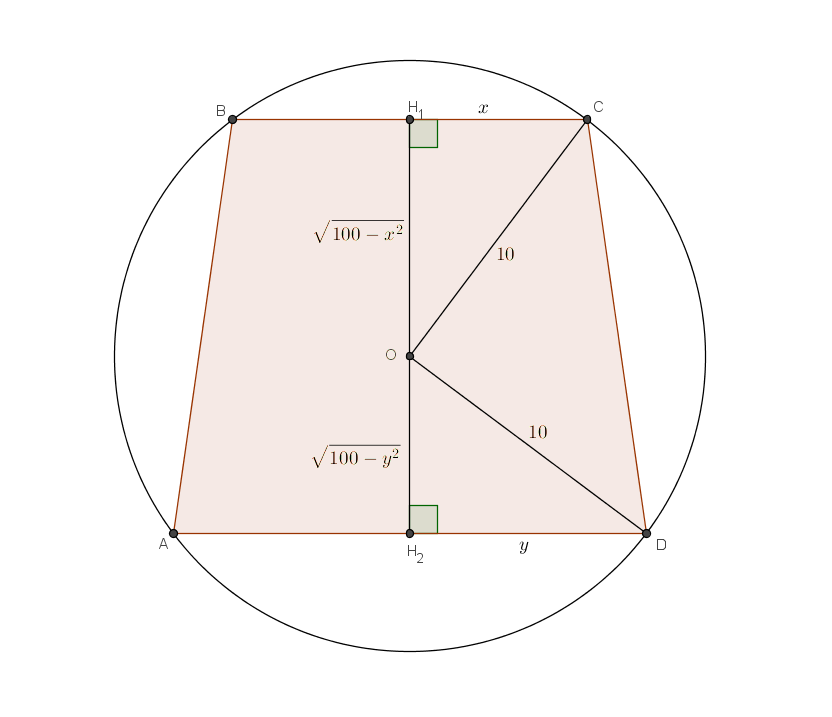
Любая вписанная трапеция равнобокая, так как углы, опирающиеся на одну дугу, должны быть равны. Обозначим основания трапеции за 2x и 2y. Тогда средняя линия равна (2x + 2y)/2 = (x + y),

Уравнения:
$begin{cases} dfrac{sqrt{100-x^2}}{sqrt{100-y^2}}=dfrac43\ x+y=sqrt{100-x^2}+sqrt{100-y^2} end{cases}$

Решаем первое уравнение.
$dfrac{sqrt{100-x^2}}{sqrt{100-y^2}}=dfrac43\ dfrac{100-x^2}{100-y^2}=dfrac{16}9\ 100-x^2=dfrac{1600}9-dfrac{16}9y^2\ x^2=dfrac{16}9y^2-dfrac{700}9$

Подставляя во второе уравнение и немного мучаясь, можно получить ответ x = 6, y = 8.

Уравнения будут выглядеть немного лучше, если обозначить куски высоты как 4x и 3x. Тогда уравнение будет выглядеть следующим образом:
$2(sqrt{100-16x^2}+sqrt{100-9x^2})=7x\ 4(200-25x^2+2sqrt{(100-16x^2)(100-9x^2)})=49x^2\ x^2=t:quad 149t-800=2sqrt{100^2-25t+144t^2}\ dots$
Получающееся квадратное уравнение радует количеством вычислений.

Наконец, можно обозначить неизвестными углы 
H1CO = x и H2DO = y
Тогда система получится простой:
$begin{cases} 4sin x=3sin y\ cos x+cos y=sin x+sin y end{cases}$
Но решать её всё равно неинтересно.

Ответ. 12, 16.