Предмет: Математика,
автор: perevoznikova16
Помогите решить уравнение, пожалуйста 
Ответы
Автор ответа:
0
Наверное услвоие таково:

4-5x=2,5 ⇒5x=1,5 ⇒x=1,5
Если все-таки верно, то что написано в задании, то

логарифмируем обе части по основанию 0,4

Получим уравнение

или

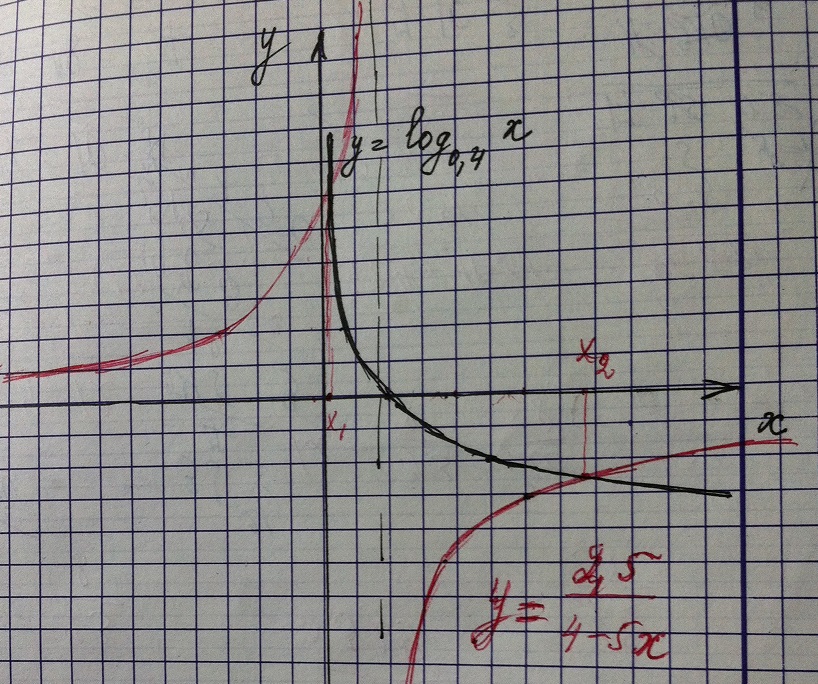
Попробуем решить графически.
(см. рисунок)
Ответ. два корня х₁≈0,1 х₂≈3,8
4-5x=2,5 ⇒5x=1,5 ⇒x=1,5
Если все-таки верно, то что написано в задании, то
логарифмируем обе части по основанию 0,4
Получим уравнение
или
Попробуем решить графически.
(см. рисунок)
Ответ. два корня х₁≈0,1 х₂≈3,8
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Aigerim1907
Предмет: Литература,
автор: geneza2009
Предмет: Математика,
автор: plis2021
Предмет: Алгебра,
автор: anjaargity
Предмет: Алгебра,
автор: Lera9703