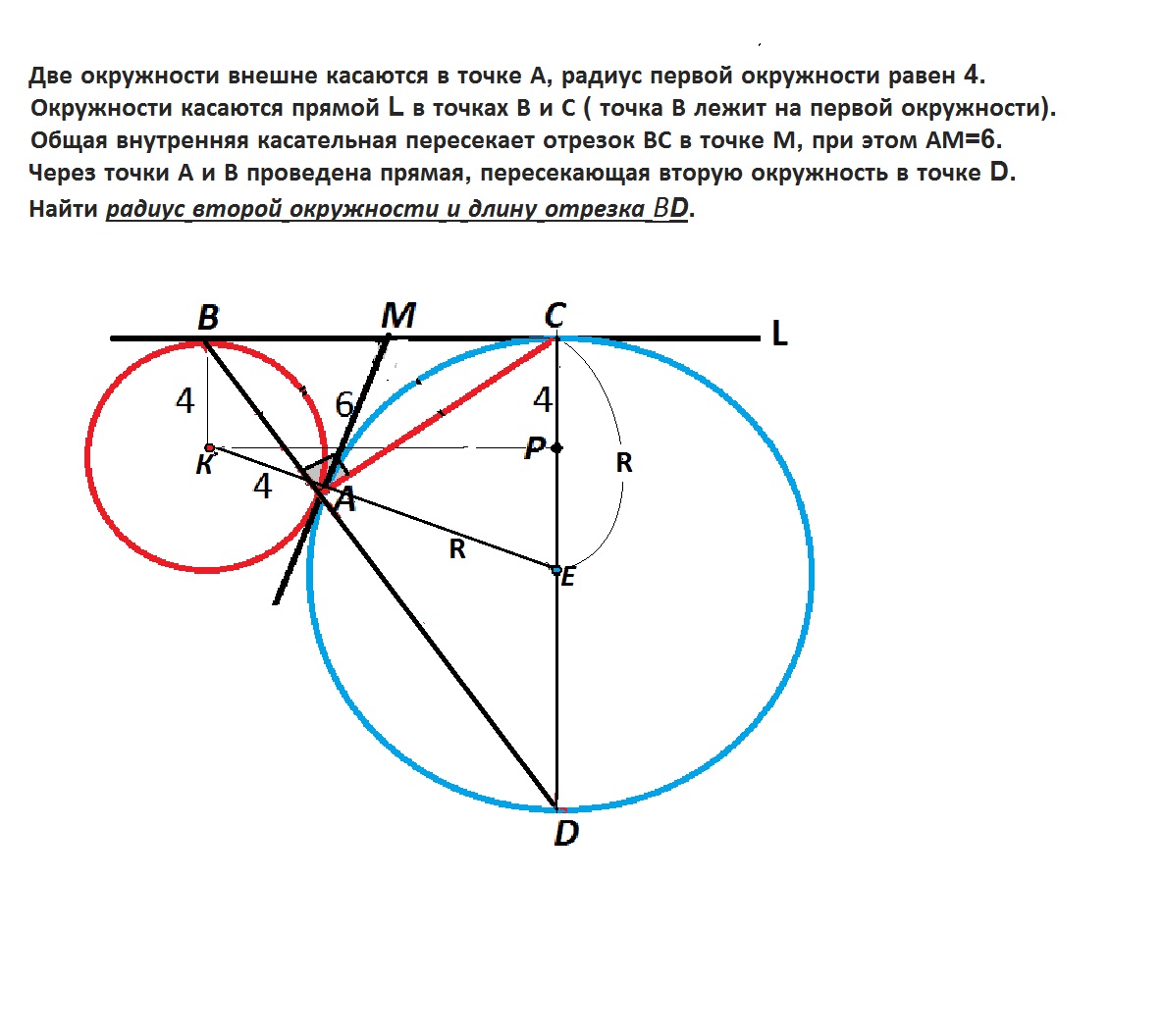
Две окружности внешне касаются в точке А, радиус первой окружности равен 4. Окружности касаются прямой L в точках В и С ( точка В лежит на первой окружности). Общая внутренняя касательная пересекает отрезок внутренняя касательная пересекает отрезок ВС в точке М, при этом АМ=6. Через точки А и В проведена прямая, пересекающая вторую окружность в точке D. Найти радиус второй окружности и длину отрезка ВD.
Ответы
Рассмотрим прямоугольный треугольник ОВМ. По Пифагору ОМ=√(ОВ²+ВМ²)=√(16+36)=√52.(ВМ=МА=МС - как касательные из одной точки к окружности). ВН - тоже высота из прямого угла и по ее свойствам (h=a*b/c) получим ВН=4*6/√52. ВА=2*ВН=48/√52.
Если из точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью. то есть ВС²=BD*BA. Или BD=ВС²/BA. ВС = ВМ+МС=12 (так как ВМ=АМ и МС=АМ - касательные из одной точки к окружности).BD = 144:ВА= 144:(48/√52) = 6√13.
Ответ: радиус второй окружности равен 9. Отрезок ВD=6√13.
P.S. Проверьте арифметику.

Вариант решения.
Обозначим центр меньшей окружности буквой К, центр большей - Е.
ВК и СЕ - радиусы этих окружностей.
Радиусы окружностей, проведенные к касательной в точку касания, образуют с ними прямой угол.
Отрезки касательных, проведенных к окружности из одной точки, равны. ⇒
ВМ=МА.
АМ=МС на том же основании.
Отсюда ВМ=МС=АМ=6
Следовательно, АМ - медиана треугольника ВАС.
Если медиана треугольника равна половине стороны, к которой проведена, то этот треугольник- прямоугольный.
Треугольник ВАС = прямоугольный, и его гипотенуза ВС=2АМ=12.
Проведем прямую КР параллельно прямой L
В прямоугольнике КВСР КР=ВС=12, угол КРЕ - прямой.
⇒ треугольник КРЕ - прямоугольный.
В нем катет КР=12, катет РЕ= R-4
Гипотенуза КЕ=r+R=4+R
По т. Пифагора выразим гипотенузу КЕ
КЕ²=КР²+РЕ²
(4+R)²=12²+(R-4)²
16+8R+R²=144+R²-8R+16
16 R=144
R=9
Так как угол ВАС=90°, смежный с ним угол САD=90°, и тогда хорда СD, на которую он опирается, - диаметр окружности и равна 2R=18
DВ найдем из прямоугольного треугольника ВСD.
DB²=BC²+CD²
BD²=144+324
BD=6√13