Предмет: Алгебра,
автор: Аноним
Помогите решить предел.
!!!С помощью замены эквивалентных БМ!!!
Приложения:
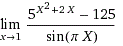
Ответы
Автор ответа:
0
Замена
х-1=t, ⇒ x=t+1


применяем замену эквивалетными бесконечно малыми
sin πt заменяем на πt

заменяем на (t²+4t)·ln5

х-1=t, ⇒ x=t+1
применяем замену эквивалетными бесконечно малыми
sin πt заменяем на πt
заменяем на (t²+4t)·ln5
Похожие вопросы
Предмет: Обществознание,
автор: peachteam150
Предмет: Математика,
автор: yavalentina1945
Предмет: Математика,
автор: vterentev881
Предмет: Алгебра,
автор: Lenok55555
Предмет: Физика,
автор: mariignusareva