Предмет: Геометрия,
автор: vlad14887
исследовать функцию и построить ее график
Приложения:
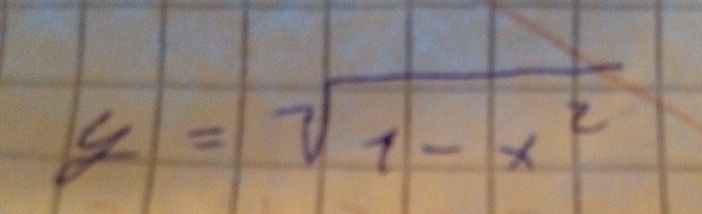
Ответы
Автор ответа:
0
Результаты исследования графика функции
x=-1.00. Точка: (-1.00, 0) x=1.00. Точка: (1.00, 0)
Экстремумы функции:Для того, чтобы найти экстремумы, нужно решить уравнение y'=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:y'=-x/sqrt(-x^2 + 1)=0
Решаем это уравнение и его корни будут экстремумами:x=0. Точка: (0, 1)
Интервалы возрастания и убывания функции: Найдем интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим на ведет себя функция в экстремумах при малейшем отклонении от экстремума: Минимумов у функции нету Максимумы функции в точках: 0 Возрастает на промежутках: (-1, 0] Убывает на промежутках: [0, 1)
Найдем точки перегибов для функции, для этого надо решить уравнение y''=0 - вторая производная равняется нулю, корни полученного уравнения будут точками перегибов указанного графика функции,
+ нужно подсчитать пределы y'' при аргументе, стремящемся к точкам неопределенности функции:y''=-x^2/(-x^2 + 1)^(3/2) - 1/sqrt(-x^2 + 1)=0
Решаем это уравнение и его корни будут точками, где у графика перегибы: Не удалось получить решение уравнения - нет перегиба. Вертикальные асимптоты Нету Горизонтальные асимптоты графика функции:Горизонтальную асимптоту найдем с помощью предела данной функции при x->+oo и x->-oo. Соотвествующие пределы находим :lim (1-x^2)^(1/2), x->+oo = oo*I, значит уравнение горизонтальной асимптоты справа: y=oo*Ilim (1-x^2)^(1/2), x->-oo = oo*I, значит уравнение горизонтальной асимптоты слева: y=oo*I Наклонные асимптоты графика функции: Наклонную асимптоту можно найти, подсчитав предел данной функции, деленной на x при x->+oo и x->-oo. Находим пределы :lim (1-x^2)^(1/2)/x, x->+oo = I, значит уравнение наклонной асимптоты справа: y=I*xlim (1-x^2)^(1/2)/x, x->-oo = -I, значит уравнение наклонной асимптоты слева: y=-I*x
Четность и нечетность функции:Проверим функцию - четна или нечетна с помощью соотношений f(x)=f(-x) и f(x)=-f(x). Итак, проверяем:(1-x^2)^(1/2) = sqrt(-x^2 + 1) - Да(1-x^2)^(1/2) = -(sqrt(-x^2 + 1)) - Нет, значит, функция является чётной
Область определения функции. ОДЗ: подкоренное выражение не может быть отрицательным, поэтому 1-x²≥0 x² ≤ 1 -1 ≤ x ≤ 1.
Точка пересечения графика функции с осью координат Y:График пересекает ось Y, когда x равняется 0: подставляем x=0 в (1-x^2)^(1/2).
Результат: y=1. Точка: (0, 1)Точки пересечения графика функции с осью координат X:График функции пересекает ось X при y=0, значит нам надо решить уравнение:(1-x^2)^(1/2) = 0 Решаем это уравнение здесь и его корни будут точками пересечения с X:x=-1.00. Точка: (-1.00, 0) x=1.00. Точка: (1.00, 0)
Экстремумы функции:Для того, чтобы найти экстремумы, нужно решить уравнение y'=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:y'=-x/sqrt(-x^2 + 1)=0
Решаем это уравнение и его корни будут экстремумами:x=0. Точка: (0, 1)
Интервалы возрастания и убывания функции: Найдем интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим на ведет себя функция в экстремумах при малейшем отклонении от экстремума: Минимумов у функции нету Максимумы функции в точках: 0 Возрастает на промежутках: (-1, 0] Убывает на промежутках: [0, 1)
Найдем точки перегибов для функции, для этого надо решить уравнение y''=0 - вторая производная равняется нулю, корни полученного уравнения будут точками перегибов указанного графика функции,
+ нужно подсчитать пределы y'' при аргументе, стремящемся к точкам неопределенности функции:y''=-x^2/(-x^2 + 1)^(3/2) - 1/sqrt(-x^2 + 1)=0
Решаем это уравнение и его корни будут точками, где у графика перегибы: Не удалось получить решение уравнения - нет перегиба. Вертикальные асимптоты Нету Горизонтальные асимптоты графика функции:Горизонтальную асимптоту найдем с помощью предела данной функции при x->+oo и x->-oo. Соотвествующие пределы находим :lim (1-x^2)^(1/2), x->+oo = oo*I, значит уравнение горизонтальной асимптоты справа: y=oo*Ilim (1-x^2)^(1/2), x->-oo = oo*I, значит уравнение горизонтальной асимптоты слева: y=oo*I Наклонные асимптоты графика функции: Наклонную асимптоту можно найти, подсчитав предел данной функции, деленной на x при x->+oo и x->-oo. Находим пределы :lim (1-x^2)^(1/2)/x, x->+oo = I, значит уравнение наклонной асимптоты справа: y=I*xlim (1-x^2)^(1/2)/x, x->-oo = -I, значит уравнение наклонной асимптоты слева: y=-I*x
Четность и нечетность функции:Проверим функцию - четна или нечетна с помощью соотношений f(x)=f(-x) и f(x)=-f(x). Итак, проверяем:(1-x^2)^(1/2) = sqrt(-x^2 + 1) - Да(1-x^2)^(1/2) = -(sqrt(-x^2 + 1)) - Нет, значит, функция является чётной
Похожие вопросы
Предмет: Українська мова,
автор: kaifonik
Предмет: Английский язык,
автор: dujsenbeksaan12
Предмет: Алгебра,
автор: kadurbekov2
Предмет: Математика,
автор: Katevan
Предмет: Алгебра,
автор: малышка88