Предмет: Алгебра,
автор: ЛешаZn
помогите решить определенный интеграл
Приложения:
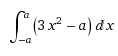
Ответы
Автор ответа:
0
найдем неопределенный интеграл. делаем замену 2х=t, dx=dt/2. интеграл J=1/2*int arccost*dt находим по частям, arccos=u, dt=dv, du=-dt/√(1-t^2), тогда J=uv-int v*du=t*arccost+int dt/√(1-t^2), в последнем интеграле делаем замену 1-t^2=y^2, dt=-y*dy/t, тогда int dt/√(1-t^2)=int dy=y+C, возвращаясь к t и x, окончательно имеем J=1/2[x*arccos2x-√(1-4x^2)]+C. надеюсь пределы подставите сами/
Автор ответа:
0
Похожие вопросы
Предмет: Қазақ тiлi,
автор: rtryuy55r5r
Предмет: Математика,
автор: aiym200835
Предмет: Математика,
автор: ajnuramangeldy235
Предмет: Алгебра,
автор: lusi1998