Предмет: Геометрия,
автор: Catwan
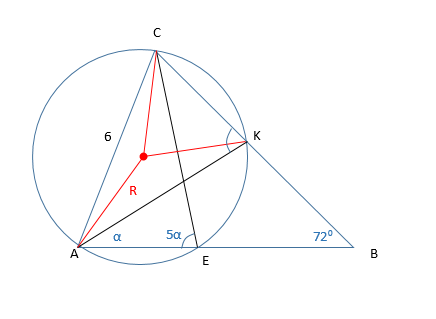
окружность проходит через вершины А и С треугольника АВС, пересекает сторону АВ в точке Е и сторону ВС в точке К. Угол АЕС в 5 раз больше угла ВАК . а угол АВС равен 72°. найти радиус окружности , если АС =6.
Ответы
Автор ответа:
0
Выполним построение.
Углы AEC и AKC вписаны в окружность и опираются на одну и ту же дугу. Значит, они равны между собой.
Угол АКС является внешним углом треугольника АКВ. Следовательно, он равен сумме двух других углов треугольника, не смежных с ним:
5α=α+72°
4α=72°
α=18°
Данная окружность описана вокруг треугольника АСК. По формуле радиуса описанной окружности, получаем:

Ответ: 3
Углы AEC и AKC вписаны в окружность и опираются на одну и ту же дугу. Значит, они равны между собой.
Угол АКС является внешним углом треугольника АКВ. Следовательно, он равен сумме двух других углов треугольника, не смежных с ним:
5α=α+72°
4α=72°
α=18°
Данная окружность описана вокруг треугольника АСК. По формуле радиуса описанной окружности, получаем:
Ответ: 3
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: Marianapi
Предмет: Английский язык,
автор: arsenukivan08
Предмет: Биология,
автор: mtv807251
Предмет: Математика,
автор: Елена5545