Question

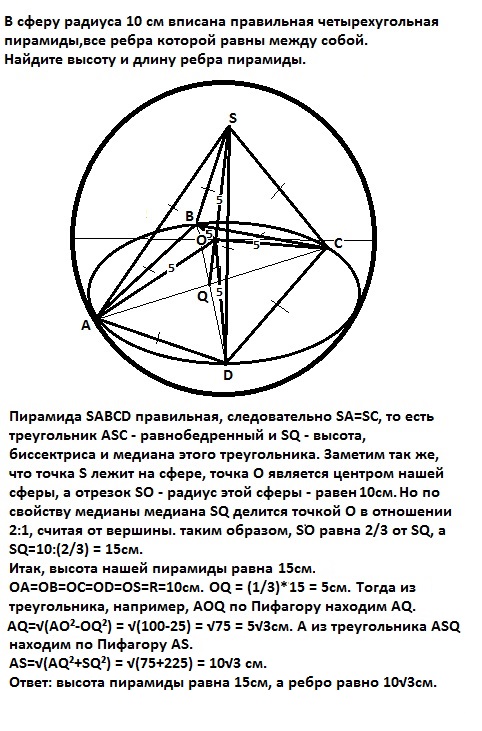
В сферу радиуса 10 см вписана правильная четырехугольная пирамиды,все ребра которой равны между собой.Найдите высоту и длину ребра пирамиды. Помогите пожалуйста))

Answer 1

Пирамида SABCD правильная, следовательно SA=SC, то есть треугольник АSC равнобедренный и SO = (2/3) от высоты SQ пирамиды. Но SO=10 см (дано).
Значит высота пирамиды равна SQ=10:(2/3) = 15 см.
Ребро пирамиды найдем по Пифагору из прямоугольных треугольников AOQ и ASQ.
OQ=(1/3)*SQ = 5cм. AQ=√(AO²-OQ²) = √(100-25) = √75 = 5√3см.
AS=√(AQ²+SQ²) = √(75+225) = 10√3 см.
Ответ: высота пирамиды равна 15см, а ребро равно 10√3см.