Предмет: Геометрия,
автор: Catwan
найти углы треугольника , которые составляют арифметическую прогрессию , если длины его сторон также составляют арифметическую прогрессию.
Ответы
Автор ответа:
0
Согласно условию, углы треугольника будут выражаться следующим образом:
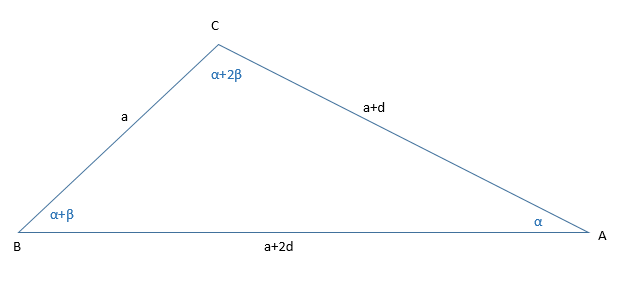
α, α+β, α+2β
где β - разность арифметической прогрессии.
По свойству углов треугольника
α+(α+β)+(α+2β)=180°
3α+3β=180°
α+β=60°
Стороны треугольника образуют арифметическую прогрессию с разностью d. Тогда их величины составляют:
a, b=a+d, c=a+2d
По теореме косинусов
b²=a²+c²-2ac cos60°
(a+d)²=a²+(a+2d)²-2a(a+2d)*0.5
a²+2ad+d²=a²+a²+4ad+4d²-a²-2ad
2ad+d²=4ad+4d²-2ad
d²=4d²
Это равенство справедливо лишь при d=0. Т.е. разность арифметической прогрессии равна 0, а это значит, что все стороны треугольника равны. Треугольник равносторонний. В свою очередь, это означает, что все углы треугольника одинаковы и равны 60°
Ответ: 60°, 60°, 60°
α, α+β, α+2β
где β - разность арифметической прогрессии.
По свойству углов треугольника
α+(α+β)+(α+2β)=180°
3α+3β=180°
α+β=60°
Стороны треугольника образуют арифметическую прогрессию с разностью d. Тогда их величины составляют:
a, b=a+d, c=a+2d
По теореме косинусов
b²=a²+c²-2ac cos60°
(a+d)²=a²+(a+2d)²-2a(a+2d)*0.5
a²+2ad+d²=a²+a²+4ad+4d²-a²-2ad
2ad+d²=4ad+4d²-2ad
d²=4d²
Это равенство справедливо лишь при d=0. Т.е. разность арифметической прогрессии равна 0, а это значит, что все стороны треугольника равны. Треугольник равносторонний. В свою очередь, это означает, что все углы треугольника одинаковы и равны 60°
Ответ: 60°, 60°, 60°
Приложения:
Похожие вопросы
Предмет: Математика,
автор: goga6943
Предмет: Қазақ тiлi,
автор: andariya2010
Предмет: Математика,
автор: svova1552
Предмет: История,
автор: Аноним