Предмет: Математика,
автор: SashaLP
Помогите пожалуйста!)
Решите производные (с подробным и понятным решением)
1) y=(arcsinx)^1/x
2) y=ln(x+(sqrtx^2+4))
Приложения:
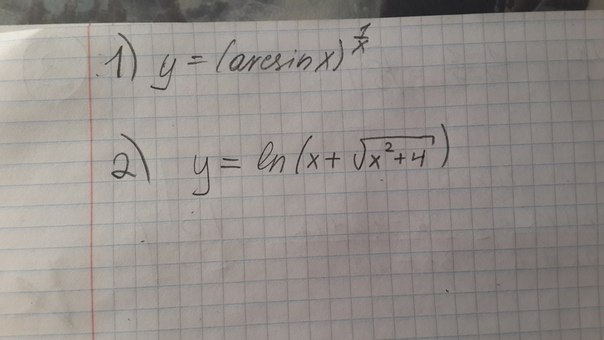
Ответы
Автор ответа:
0
y=(arcsinx)^(1/x)=e^(ln(arcsin(x))/x)
y`=e^(ln(arcsin(x))/x) * (ln(arcsin(x))/x)` =
= (arcsinx)^(1/x) * [ (ln(arcsin(x))` * x - (ln(arcsin(x)) * x` ] / x^2 =
= (arcsinx)^(1/x) * [ (x*(arcsin(x))`/arcsin(x) - (ln(arcsin(x)) ] / x^2 =
= (arcsinx)^(1/x) * [ (x/корень(1-x^2) *1/arcsin(x) - (ln(arcsin(x)) ] / x^2
y=ln(x+(sqrtx^2+4))
y`=1/(x+(sqrtx^2+4)) * (x+(sqrtx^2+4))` =
=1/(x+(sqrtx^2+4)) * (1+1/2*1/корень(x^2+4)*(x^2+4)') =
=1/(x+(sqrtx^2+4)) * (1+1/2*1/корень(x^2+4)*2х) =
=1/(x+(sqrtx^2+4)) * (1+х/корень(x^2+4)) =
=1/(x+(sqrtx^2+4)) * (корень(x^2+4)+х)/корень(x^2+4) =
=1/корень(x^2+4)
y`=e^(ln(arcsin(x))/x) * (ln(arcsin(x))/x)` =
= (arcsinx)^(1/x) * [ (ln(arcsin(x))` * x - (ln(arcsin(x)) * x` ] / x^2 =
= (arcsinx)^(1/x) * [ (x*(arcsin(x))`/arcsin(x) - (ln(arcsin(x)) ] / x^2 =
= (arcsinx)^(1/x) * [ (x/корень(1-x^2) *1/arcsin(x) - (ln(arcsin(x)) ] / x^2
y=ln(x+(sqrtx^2+4))
y`=1/(x+(sqrtx^2+4)) * (x+(sqrtx^2+4))` =
=1/(x+(sqrtx^2+4)) * (1+1/2*1/корень(x^2+4)*(x^2+4)') =
=1/(x+(sqrtx^2+4)) * (1+1/2*1/корень(x^2+4)*2х) =
=1/(x+(sqrtx^2+4)) * (1+х/корень(x^2+4)) =
=1/(x+(sqrtx^2+4)) * (корень(x^2+4)+х)/корень(x^2+4) =
=1/корень(x^2+4)
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: batyrbekovbd
Предмет: Қазақ тiлi,
автор: cernozubenkoirina
Предмет: Математика,
автор: shatirina1999