Question

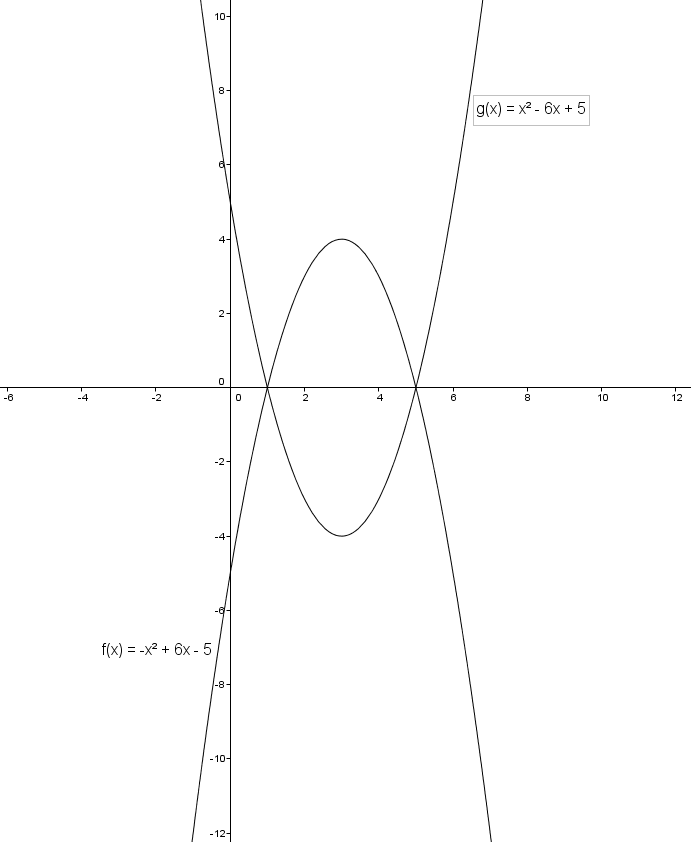
Дана функция -x^2+6x-5. Можно ли умножить на (-1)? Совсем другой график почему-то получается. Ветви должны быть вниз направлены. Помогите, пожалуйста!!!

Answer 1

Стандартный вид квадратичной функции:
$y=ax^{2}+bx+c$

$f(x)=-x^{2}+6x-5 \ D=36-4*(-1)*(-5)=16=4^{2} \ x_{1}= frac{-6-4}{-2}=5 \ x_{2}= frac{-6+4}{-2}=1$

При a < 0 ветви параболы направлены вниз.

Приведём функцию в стандартный вид, умножив функцию на -1.

$g(x)=x^{2}-6x+5 \ D=36-4*1*5=16=4^{2} \ x_{1}= frac{6-4}{2}=1\ x_{2}=frac{6+4}{2}=5$

При a > 0 ветви параболы направлены вверх.

Answer 2

Выделим полный квадрат
y=-x^2+6x-5=-(x^2-6x+9-9+5)=-(x^2-6x+9)+9-5=-(x-3)^2+4
Ветви параболы направлены вниз. Этот график можно получить смещением параболы y=-x^2 на 3 единицы вправо и на 4 - вверх
O(3;4) - вершина параболы

Answer 3

Спасибо большое, я нашла свою ошибку! Я не так нашла вершину параболы. У меня получилось, что она находится в точке (3;22), то есть я не учла того, что перед х стоит минус.