Question

Дана функция f(x)=2х-3∛(х^2 )
Найти:
а)Критические точки функции f(x) на отрезке [-1;8]
б)Наибольшее и наименьшее значение функции f(x) на отрезке [-1;8]

Answer 1

$tt displaystyle f(x)=2x-3cdot sqrt[3]{x^2} \f'x)=(2x)'-3(x^{frac23 }) '=2-3cdot frac23 cdot x^{-frac13 } =\=2-frac2{sqrt[3]{x} } =frac{2cdot sqrt[3]{x} -2}{sqrt[3]{x}} =frac{2(sqrt[3]{x} -1}{sqrt[3]{x} }$

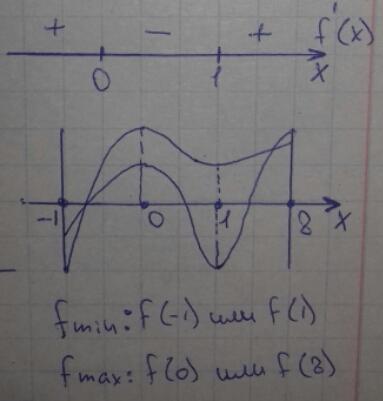
а) Критические точки:

$tt displaystyle begin{Bmatrix}begin{bmatrix}sqrt[3]{x} -1=0\sqrt[3]{x} =0end{matrix} \xin [-1;8]end{matrix}quad begin{Bmatrix}begin{bmatrix}sqrt[3]{x} =1\x=0end{matrix}\xin [-1;8]end{matrix}\\begin{Bmatrix}x={0;1}\xin [-1;8]end{matrix}qquad x={0;1}.$

б) $tt displaystyle f_{min},f_{max},xin [-1;8]-?$

f(-1) = 2·(-1)-3·$sqrt[3]{(-1)^2}$ = -2-3 = -5

f(1) = 2·1-3·$sqrt[3]{1^2}$ = 2-3 = -1

-5 < -1 ⇒ $tt displaystyle f_{min} =f(-1)=-5$

f(0) = 2·0-3·$sqrt[3]{0^2}$ = 0-0 = 0

f(8) = 2·8-3·$sqrt[3]{8^2}$ = 16-3·$sqrt[3]{2^6}$ = 16-12 = 4

4 > 0 ⇒ $tt displaystyle f_{max} =f(8)=4$

Ответ: а) x = {0;1}; б) $tt displaystyle f_{min} =-5,f_{max} =4.$