Предмет: Алгебра,
автор: renta123456789
помогите решить уравнение
Приложения:
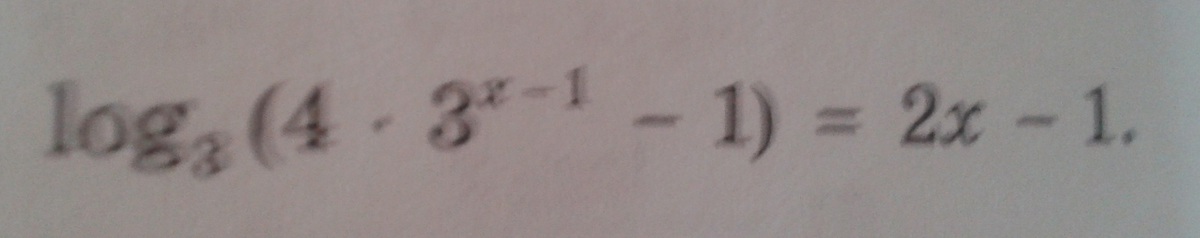
Ответы
Автор ответа:
0
Формулы: a^(m-n)=a^m/a^n
log3(4*3^(x-1)-1)=2x-1⇒3^(2x-1)=4*3^(x-1)-1⇒3^(2x)/3=4*3^x/3-1
Умножаем обе части на 3:
3^(2x)=4*3^x-3⇒3^(2x)-4*3^x+3=0
Замена: 3^x=t⇒t^2-4t+3=0⇒по теореме Виетта t1+t2=4; t1*t2=3⇒t1=1; t2=3⇒
3^x=1⇒3^x=3^0⇒x1=0
3^x=3⇒3^x=3^1⇒x2=1
Проверка
1) x=0⇒log3(4*3^(0-1)-1)=log3(4*3^(-1)-1)=log3(4/3-1)=log3(1/3)=-1
2x-1=2*0-1=-1⇒левая и правая части равны
2) x=1⇒log3(4*3^(1-1)-1)=log3(4*3^0-1)=log3(4-1)=log3(3)=1
2x-1=2*1-1=1⇒левая и правая части равны
log3(4*3^(x-1)-1)=2x-1⇒3^(2x-1)=4*3^(x-1)-1⇒3^(2x)/3=4*3^x/3-1
Умножаем обе части на 3:
3^(2x)=4*3^x-3⇒3^(2x)-4*3^x+3=0
Замена: 3^x=t⇒t^2-4t+3=0⇒по теореме Виетта t1+t2=4; t1*t2=3⇒t1=1; t2=3⇒
3^x=1⇒3^x=3^0⇒x1=0
3^x=3⇒3^x=3^1⇒x2=1
Проверка
1) x=0⇒log3(4*3^(0-1)-1)=log3(4*3^(-1)-1)=log3(4/3-1)=log3(1/3)=-1
2x-1=2*0-1=-1⇒левая и правая части равны
2) x=1⇒log3(4*3^(1-1)-1)=log3(4*3^0-1)=log3(4-1)=log3(3)=1
2x-1=2*1-1=1⇒левая и правая части равны
Похожие вопросы
Предмет: Алгебра,
автор: cherryjuice26
Предмет: Қазақ тiлi,
автор: malimov
Предмет: Алгебра,
автор: eka1388
Предмет: Математика,
автор: mischlen1