Предмет: Алгебра,
автор: heimister
Помогите решить уравнение через ОДЗ и что то такое.
Приложения:
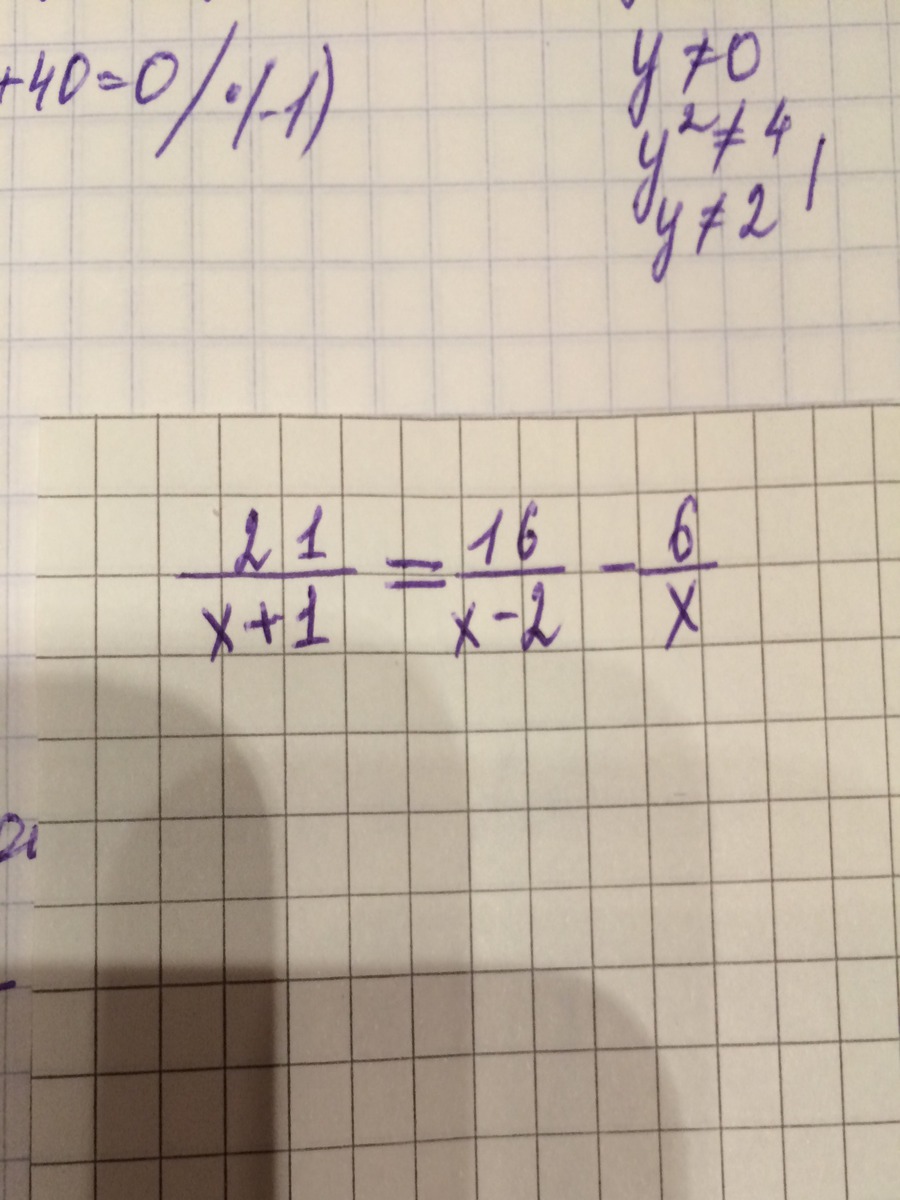
Ответы
Автор ответа:
0
ОДЗ в этом примере получается из условия "на ноль делить нельзя":



Далее, приводим к общему знаменателю:






Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.
Решаем обычное квадратное уравнение:

D= 4096 + 528 = 4624 =
 - подходит по ОДЗ
- подходит по ОДЗ
 - подходит по ОДЗ
- подходит по ОДЗ
Ответ: -2/11 и 6
Далее, приводим к общему знаменателю:
Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.
Решаем обычное квадратное уравнение:
D= 4096 + 528 = 4624 =
Ответ: -2/11 и 6
Похожие вопросы
Предмет: Алгебра,
автор: rtmkbzr
Предмет: Алгебра,
автор: DeViLiNkEdS
Предмет: Математика,
автор: vadimoliynuk10
Предмет: Физика,
автор: Тёмка10
Предмет: Информатика,
автор: groonel