Question

Докажите, что геометрическое место точек M, из которых отрезок AB виден под острым углом (угол AMB<90°) есть внешность круга с диаметром AB без точек прямой AB

Answer 1

Впрочем, наверное можно вот как доказать:
1) Отрезок АВ виден под прямым углом из точек, расположенных на самой окружности, т.к. вписанный угол, опирающийся на диаметр равен 90 градусов.
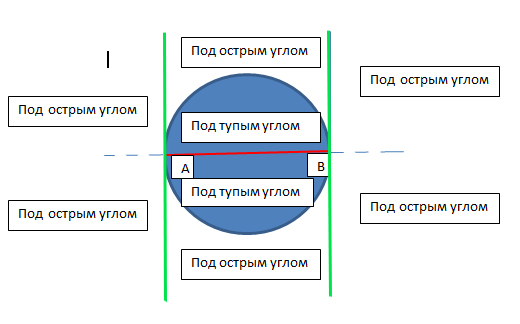
2) на рисунке видны зеленоватые линии, перпендикулярные к отрезку АВ - очевидно, что если точка М лежит на этих прямых, то треугольник ABM прямоугольный и отрезок AB как катет виден из точки М под острым углом.
3) Если точа М оказывается не между этих прямых, а снаружи, то очевидно, что треугольник ABM тупоугольный и стало быть опять же отрезок AB виден из точки М под острым углом
4) Если точка М оказывается вне окружности и между этих зеленоватых прямых, то отрезок АВ виден под острым углом, так как по свойству угла внешнего к окружности он измеряется полуразностью дуг, высекаемых из окружности. Одна дуга - ВА равна 180 градусов, и её половина равна 90 градусов, а другая дуга - пусть даже самая маленькая всё равно что-то да будет из этих 90 градусов отнимать => отрезок АВ будет виден под острым углом