Question

В правильную треугольную пирамиду со стороной основания корень из 3 вписан цилиндр, осевое сечение которого является квадратом. Высота пирамиды равна 3. Найдите площадь боковой поверхности цилиндра.

Answer 1

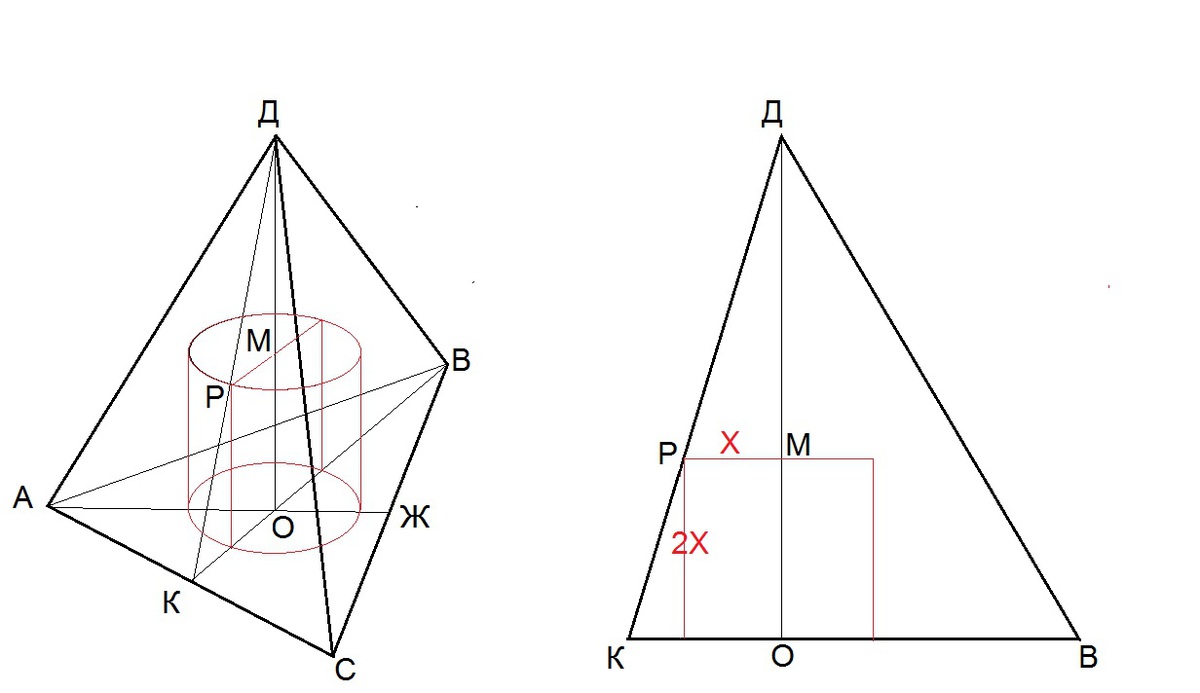
 КВ и АЖ -медианы основания пирамиды. Р - точка касания цилиндра грани пирамиды. Рассечем пирамиду плоскостью, проходящей через точки ДКВ.  Эта секущая плоскость пройдет через медиану основания пирамиды и через ось цилиндра. Значит в этой плоскость сечения  цилиндра изобразится в виде квадрата.( цилиндр и плоскость его сечения изображены красным цветом).  Поскольку пирамида правильная, то в её основании лежит равносторонний треугольник. В таком треугольнике медиана КВ является и высотой на АС.  Значит КВ = √(ВС² - КС²) = √(3 - 3/4) = √9/4 = 3/2. КО = трети от ВК = (3/2)/3 =0,5. Радиус цилиндра - РМ обозначим Х. Высота цилиндра 2Х. Из подобия треугольников ДОК и ДМР  следует, что  ДО/ОК = ДМ/МР или 3/0,5 = (3-2Х)/Х, или 3Х = 1,5 - Х, или 4Х=1,5. Отсюда Х=1,5/4 =3/8.  Площадь боковой поверхности цилиндра = π2Х×2Х = π4 X² = π16*9/64 = 2,25π