Question

найдите площадь равнобедренной трапеции если ее диагональ равная 5 образует с основанием угол синус которого равен 0,6

Answer 1

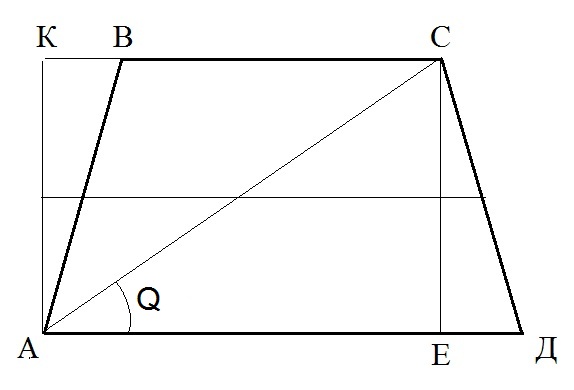
На рисунке во вложении видно, что площадь трапеции АВСД равна площади прямоугольника АКСЕ, т.к. площадь треугольника СДЕ равна площади треугольника АКВ. Таким образом площадь трапеции равна СЕ×АЕ = АС×sinQ×АС×cosQ = АС²sinQ×cosQ = АС² sinQ√(1- sin²Q) = 25×0,6×0,8= 12 неизвестно каких квадратных единиц.

Answer 2

Пусть АВСД данная равнобедренная трапеция, тогда её площадь равна полупроизведению оснований на высоту. Проведём СК высоту, тогда из треугольника АСК СК=АСумножить на sinCAD  СК=5.0,6=3. Треугольник АСК - Египетский, следовательно АК=4. Т.К. трапеция равнобедренная, то( АВ+ВС):2=АК=4. Площадь равнв 4*3=12.