Question

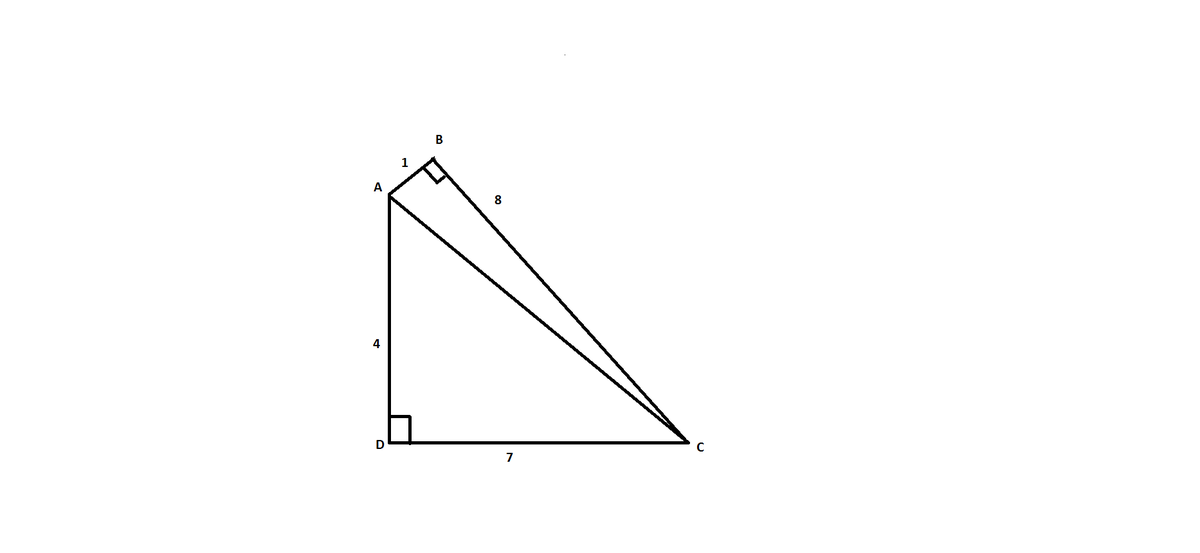
Какова наибольшая возможная площадь четырехугольника ABCD, стороны которого равны AB=1, BC=8, CD=7,DA=4?

Answer 1

SABCD=SABC+SACD=1/2*8*1*sinB+1/2*7*4*sinD=2*(2*sinB+7*sinD)
  Чем больше косинусы ,тем выше значение выражения.
Заметим  что:
AB^2+BC^2=8^2+1^2=AD^2+CD^2=7^2+4^2=65
То  если угол B прямой,то раз  cторона AC общая,то и угол D будет  прямым  из  обратной  теоремы Пифагора.
То sinB=sinD=1.
Очевидно  что при данных синусах  площадь будет наибольшей  поскольку: sinB<=1 ,sinD<=1
Откуда Smax=2*(2+7)=18
Ответ:Smax=18.