Предмет: Математика,
автор: kondan4
Подобие треугольников, СРОЧНО! Заранее благодарю! ЛЮБЫЕ из 4 задач! (желательно все, конечно)
1) Дано:
ΔA₁B₁C₁~ΔABC
A₁B₁=3
B₁C₁=4
A₁C₁=6
PΔABC=78
Найти:
AB, AC, BC - ?
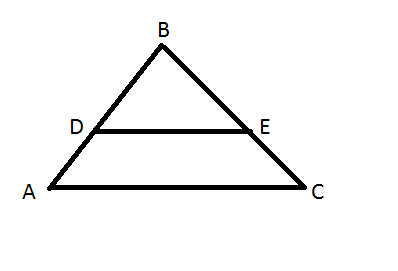
2) Дано: (по первому чертежу)
ΔABC
DEIIAC (параллельно)
AB=18
BD=9
AC=8
Найти:
DE - ?
3) Дано: (по второму чертежу)
ΔABC
∠C=90'
CD - высота
CB=6
AB=18
Найти:
AB, BD, CD, AC - ?
4)Дано: (по второму чертежу)
ΔABC
∠C=90'
AD=4
BD=9
CD - высота
Найти:
CD, AC, BC - ?
Еще раз - Спасибо!
Приложения:

Ответы
Автор ответа:
0
1.
так как треугольники подобны, то их соответствующие стороны пропорциональны.
Р (А1В1С1) = А1В1+В1С1+А1С1 = 3+4+6=13 см
Р (АВС)= 78, значит все стороны етого треугольника больше сторон треугольника А1В1С1 в 6 раз (78/13=6 раз), значит:
АВ=3*6=18см, ВС=4*6=24см, АС=6*6=36 см
2.
так как АС параллельно ДЕ, то треугольники АВС и ДВЕ подобны, значит:
АВ:ВД=АС:ДЕ
ДЕ=(ВД*АС)/АВ=9*8/18=4см
так как треугольники подобны, то их соответствующие стороны пропорциональны.
Р (А1В1С1) = А1В1+В1С1+А1С1 = 3+4+6=13 см
Р (АВС)= 78, значит все стороны етого треугольника больше сторон треугольника А1В1С1 в 6 раз (78/13=6 раз), значит:
АВ=3*6=18см, ВС=4*6=24см, АС=6*6=36 см
2.
так как АС параллельно ДЕ, то треугольники АВС и ДВЕ подобны, значит:
АВ:ВД=АС:ДЕ
ДЕ=(ВД*АС)/АВ=9*8/18=4см
Автор ответа:
0
3 и 4 к сожалению не знаю как решить. извини)))
Автор ответа:
0
Благодарю ;)
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: История,
автор: Аноним
Предмет: Алгебра,
автор: telenkovauy
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: DIMAH228