Предмет: Алгебра,
автор: ZiZaFoReVeR
Найти производную функции
Приложения:
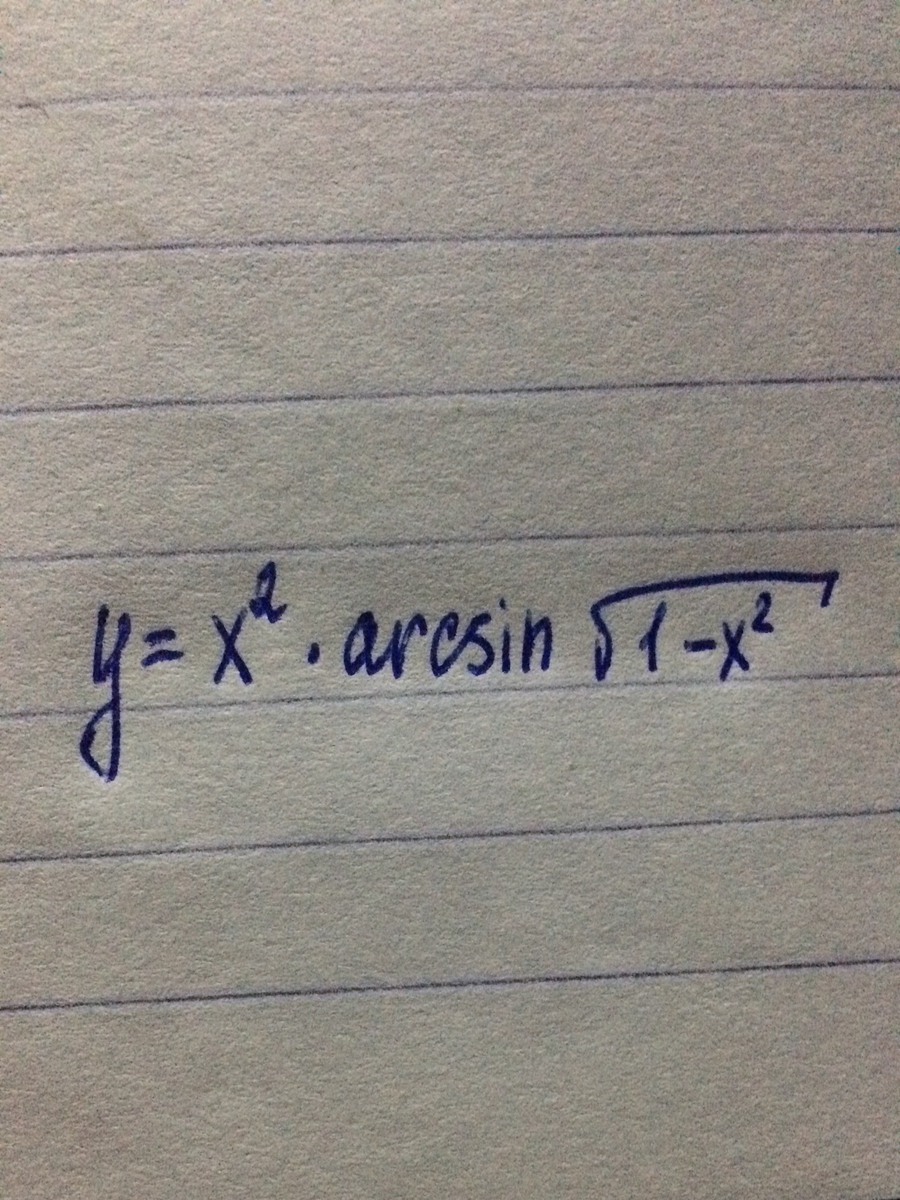
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Химия,
автор: aayyaazz
Предмет: Математика,
автор: Alexalina12
Предмет: Английский язык,
автор: nahmadillaevadamira
Предмет: Математика,
автор: svetusik8383
Предмет: Математика,
автор: doc34