Предмет: Алгебра,
автор: malivina76
Решите тригонометрическое неравенство:
Приложения:
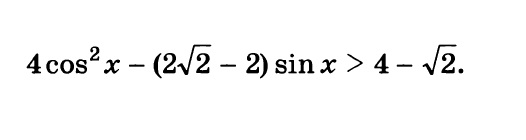
Ответы
Автор ответа:
0
4(1-sin²x)-(2√2-2)-4+√2>0
4-4sin²x-(2√2-2)sinx-4+√2>0
4sin²x+(2√2-√)sinx-√2<0
sinx=a
4a²+(2√2-2)a-√2<0
D=8-8√2+4+16√2=8*8√2+4=(2√2+2)²
√D=2√2+2
a1=(2-2√2-2√2-2)/8=-√2/2
a2=(2-2√2+2√2+2)/8=1/2
-√2/2<a<1/2⇒-√2/2<sinx<1/2
x∈(-π/4+2πn;π/6+2πn) U (5π/6+2πn;5π/4+2πn)
4-4sin²x-(2√2-2)sinx-4+√2>0
4sin²x+(2√2-√)sinx-√2<0
sinx=a
4a²+(2√2-2)a-√2<0
D=8-8√2+4+16√2=8*8√2+4=(2√2+2)²
√D=2√2+2
a1=(2-2√2-2√2-2)/8=-√2/2
a2=(2-2√2+2√2+2)/8=1/2
-√2/2<a<1/2⇒-√2/2<sinx<1/2
x∈(-π/4+2πn;π/6+2πn) U (5π/6+2πn;5π/4+2πn)
Автор ответа:
0
вот почему удалили мой ответ
22:56 zsedina отметила нарушение в решении Пользователя IUV
22:56 zsedina отметила нарушение в решении Пользователя IUV
Автор ответа:
0
4cos^2(x)-(2*корень(2)-2)*sin(x) >4-корень(2)
4(1-sin^2(x))-(2*корень(2)-2)*sin(x) >4-корень(2)
4-4sin^2(x))-(2*корень(2)-2)*sin(x) >4-корень(2)
-4sin^2(x))-(2*корень(2)-2)*sin(x) >-корень(2)
4sin^2(x))+(2*корень(2)-2)*sin(x) -корень(2)<0
-корень(2)/2 <sin(x)<1/2
x є (5pi/6+2*pi*k;5pi/4+2*pi*k) U (-pi/4+2*pi*k; pi/6+2*pi*k)
4(1-sin^2(x))-(2*корень(2)-2)*sin(x) >4-корень(2)
4-4sin^2(x))-(2*корень(2)-2)*sin(x) >4-корень(2)
-4sin^2(x))-(2*корень(2)-2)*sin(x) >-корень(2)
4sin^2(x))+(2*корень(2)-2)*sin(x) -корень(2)<0
-корень(2)/2 <sin(x)<1/2
x є (5pi/6+2*pi*k;5pi/4+2*pi*k) U (-pi/4+2*pi*k; pi/6+2*pi*k)
Автор ответа:
0
Но ведь и была ошибка!
Похожие вопросы
Предмет: Математика,
автор: narmetovasilbek2
Предмет: Биология,
автор: alimpiagood52
Предмет: Английский язык,
автор: dastu
Предмет: Геометрия,
автор: Глебыч2000
Предмет: Химия,
автор: Venerkavi