Question

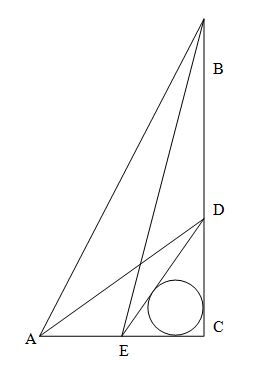
В треугольнике АВС проведены биссектрисы АД и СЕ. Найдите радиус вписанной окружности в треугольнике ВДЕ, если АС = 60, АЕ = 20, СД = 30.

Answer 1

Биссектриса треугольника делит противоположную сторону на отрезки пропорциональные двум другим сторонам, т.е.:
$frac{AC}{CD} = frac{AB}{CB}$ и  $frac{AC}{AE} = frac{CB}{EB}$
Пусть EB = x, BD = y. Получим 2 уравнения:
$left { {{ frac{60}{30} = frac{20+x}{y}} atop {frac{60}{20} = frac{30+y}{x}}} right. ; left { {{2y=20+x} atop {3x=30+y}} right. ; left { {{x=2y-20} atop {6y-60=30+y}} right. ; left { {{x=16} atop {y=18}} right. .$
EB = 16; BD = 18, тогда
АВ = 20 + 16 = 36
ВС = 30 + 18 = 48
Заметим, как относятся стороны треугольника АВС:
АВ : ВС : АС = 60 : 48 : 36 = 5 : 4 : 3 - египетский треугольник, т.е. ΔАВС - прямоугольный с прямым углом В.
Тогда ΔЕВD - так же прямоугольный, его катеты равны 16 и 18, найдем гипотенузу ED:
$ED = sqrt{16^2+18^2} = sqrt{256+324} = sqrt{580} = 2<span>sqrt{145}</span>$
Площадь прямоугольного ΔЕВD:
S = EB * BD /2 = 16*18/2 = 144
Полупериметр ΔЕВD:
p = (EB + BD + ED)/2 = (16+18+2√145)/2 = (34 + 2√145)/2 = 17 + √145
радиус вписанной окружности:
r = S / p = 144/(17+√145) = 17-√145

Answer 2

А почему у Вас проведена биссектриса ВЕ, а не СЕ, как по условию?

Answer 3

На чертеже перепутал обозначения (С и В), но решение правильное, по условию

Answer 4

просто на чертеже поменяйте буквы В и С местами