Question

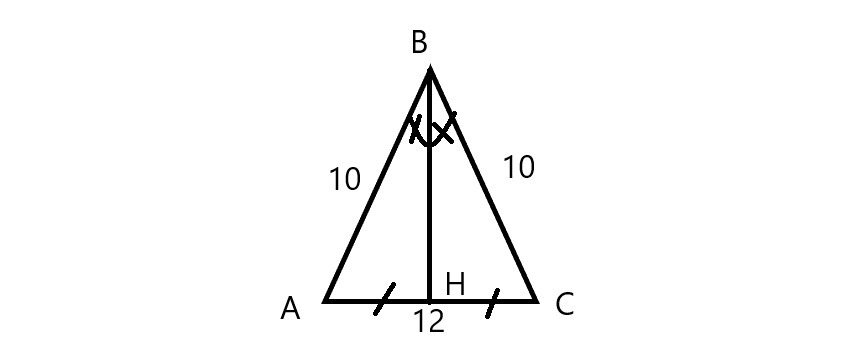
В равнобедренном треугольнике АВС АВ=ВС=10, АС=12, найдите синус угла В. Помогите плиз

Answer 1

Проведем высоту из вершины В. Она также является медианой и биссектрисой.
Рассматриваем треугольник АВН - прямоугольный, гипотенуза АВ=10, катет АН=АС/2=12/2=6, второй катет ВН по т. Пифагора √(10²-6²)=8;
в треугольнике АВН синус угла В - АН/АВ=6/10=0,6;
косинус угла В - АН/АВ=8/10=0,8;
В треугольнике АВС угол В равен двум углам В в треугольнике АВН;
sin2B=2sinB*cosb=2*0.6*0.8=0.96.

Answer 2

по теореме косинусов
12² = 10² + 10² -2·10·10·сos α
сjs α  = 0,28
sin α = √(1 - 0,28²) = 0,96