Предмет: Математика,
автор: 1234554321R
Помогите, пожалуйста)
Приложения:
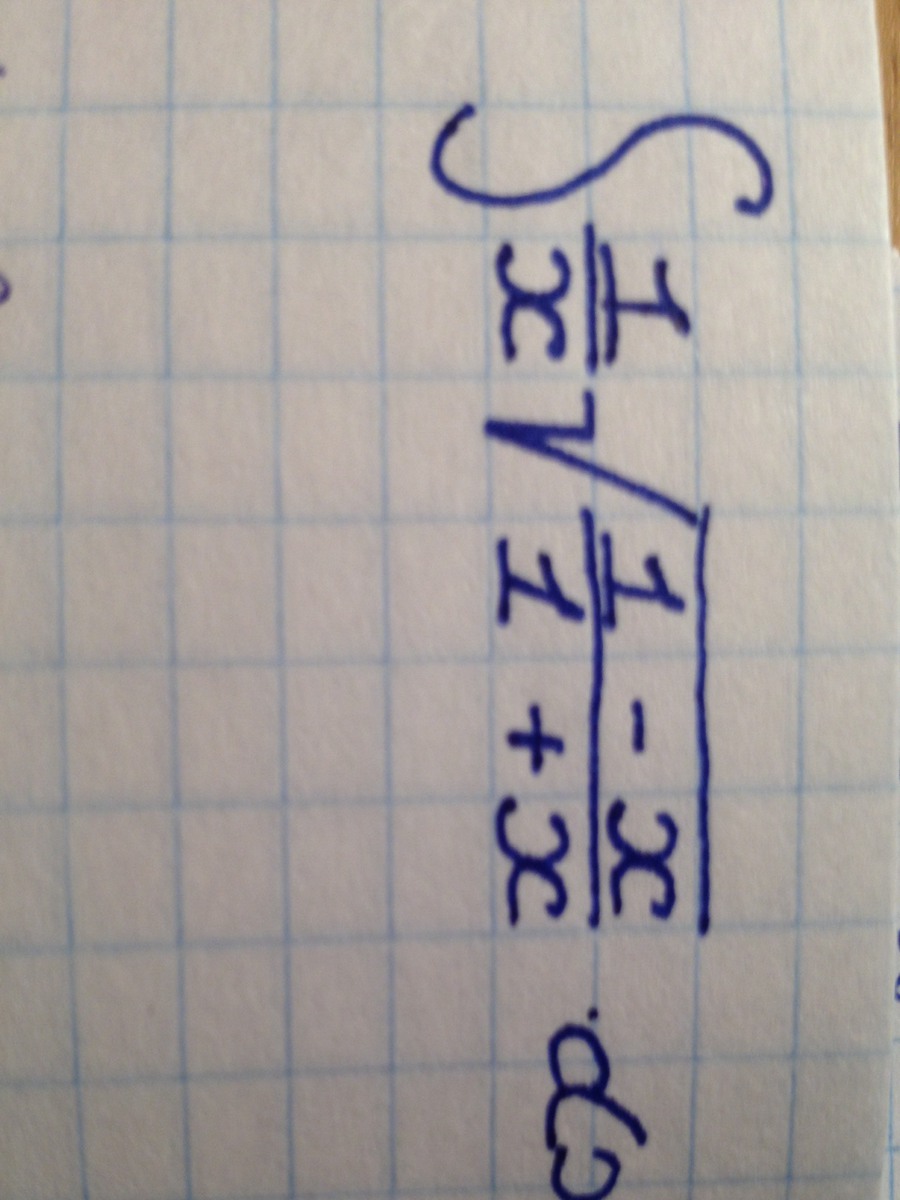
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Физика,
автор: dimashkonysov0
Предмет: Математика,
автор: BSVeNoM
Предмет: Английский язык,
автор: Аноним
Предмет: Химия,
автор: nelly1029
Предмет: Биология,
автор: natusik3308