Предмет: Алгебра,
автор: namazbek23
Решите систему уравнений
Приложения:
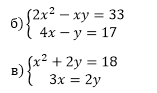
Ответы
Автор ответа:
0
б) 2х²-ху=33 Эту систему решаем методом подстановки:
4х-у=17 у = 4х-17 подставляем в первое уравнение:
2х²-х(4х-17)-33 = 0
2х²-4х²+17х-33 = 0
-2х²+17х-33 = 0
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=17^2-4*(-2)*(-33)=289-4*(-2)*(-33)=289-(-4*2)*(-33)=289-(-8)*(-33)=289-(-8*(-33))=289-(-(-8*33))=289-(-(-264))=289-264=25;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√25-17)/(2*(-2))=(5-17)/(2*(-2))=-12/(2*(-2))=
= -12/(-2*2)=-12/(-4)=-(-12/4)=-(-3)=3;
x_2=(-√25-17)/(2*(-2))=(-5-17)/(2*(-2))=-22/(2*(-2))=
= -22/(-2*2)=-22/(-4)=-(-22/4)=-(-5.5)=5.5.
в) х² + 2у = 18 Решаем методом сложения с изменением знаков 2у = 3х второго уравнения:
х² + 2у-18 = 0
3х - 2у = 0
х² + 3х -18 = 0
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=3^2-4*1*(-18)=9-4*(-18)=9-(-4*18)=9-(-72)=9+72=81;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√81-3)/(2*1)=(9-3)/2=6/2=3;
x_2=(-√81-3)/(2*1)=(-9-3)/2=-12/2=-6.
4х-у=17 у = 4х-17 подставляем в первое уравнение:
2х²-х(4х-17)-33 = 0
2х²-4х²+17х-33 = 0
-2х²+17х-33 = 0
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=17^2-4*(-2)*(-33)=289-4*(-2)*(-33)=289-(-4*2)*(-33)=289-(-8)*(-33)=289-(-8*(-33))=289-(-(-8*33))=289-(-(-264))=289-264=25;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√25-17)/(2*(-2))=(5-17)/(2*(-2))=-12/(2*(-2))=
= -12/(-2*2)=-12/(-4)=-(-12/4)=-(-3)=3;
x_2=(-√25-17)/(2*(-2))=(-5-17)/(2*(-2))=-22/(2*(-2))=
= -22/(-2*2)=-22/(-4)=-(-22/4)=-(-5.5)=5.5.
в) х² + 2у = 18 Решаем методом сложения с изменением знаков 2у = 3х второго уравнения:
х² + 2у-18 = 0
3х - 2у = 0
х² + 3х -18 = 0
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=3^2-4*1*(-18)=9-4*(-18)=9-(-4*18)=9-(-72)=9+72=81;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√81-3)/(2*1)=(9-3)/2=6/2=3;
x_2=(-√81-3)/(2*1)=(-9-3)/2=-12/2=-6.
Похожие вопросы
Предмет: Русский язык,
автор: hFaguagagu
Предмет: Математика,
автор: zabivnojmolodoj
Предмет: Английский язык,
автор: alekseenkonadezda7
Предмет: Математика,
автор: люба040204д