Предмет: Алгебра,
автор: нкиа
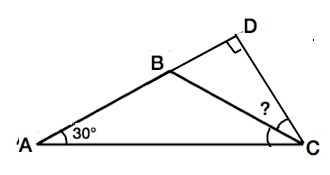
В тупоугольном треугольнике ABC AB=BC,угол А равен 30 градусов,СD - высота, проведённая из вершины С.Найдите градусную меру угла BCD.
Ответы
Автор ответа:
0
Треугольник АВС равнобедренный, АС - основание. угол С=А=30°.
Угол В=180°-30°•2=120°
∆ АВС тупоугольный, поэтому высота, проведенная из вершины острого угла ляжет вне треугольника и пересечет продолжение боковой стороны. .
Треугольник АСD - прямоугольный.
Сумма острых углов прямоугольного треугольника 90°. ⇒
Угол АСD=90°-30°=60°
Угол BCD=∠ACD-∠ACB=60°-30°=30°
---------
Решение будет несколько иным, если
1)найти угол АВС,
2) смежный ему угол СВD и затем
3) из прямоугольного ∆ BCD найти нужный угол с тем же результатом =30°
Угол В=180°-30°•2=120°
∆ АВС тупоугольный, поэтому высота, проведенная из вершины острого угла ляжет вне треугольника и пересечет продолжение боковой стороны. .
Треугольник АСD - прямоугольный.
Сумма острых углов прямоугольного треугольника 90°. ⇒
Угол АСD=90°-30°=60°
Угол BCD=∠ACD-∠ACB=60°-30°=30°
---------
Решение будет несколько иным, если
1)найти угол АВС,
2) смежный ему угол СВD и затем
3) из прямоугольного ∆ BCD найти нужный угол с тем же результатом =30°
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: olgazaboeva
Предмет: Химия,
автор: Millymiller
Предмет: Физика,
автор: 80916
Предмет: Математика,
автор: ВиКуСьКкКа
Предмет: Математика,
автор: dh3jybrf