Предмет: Алгебра,
автор: bekkaaa
Помогите решить уравнение
Приложения:
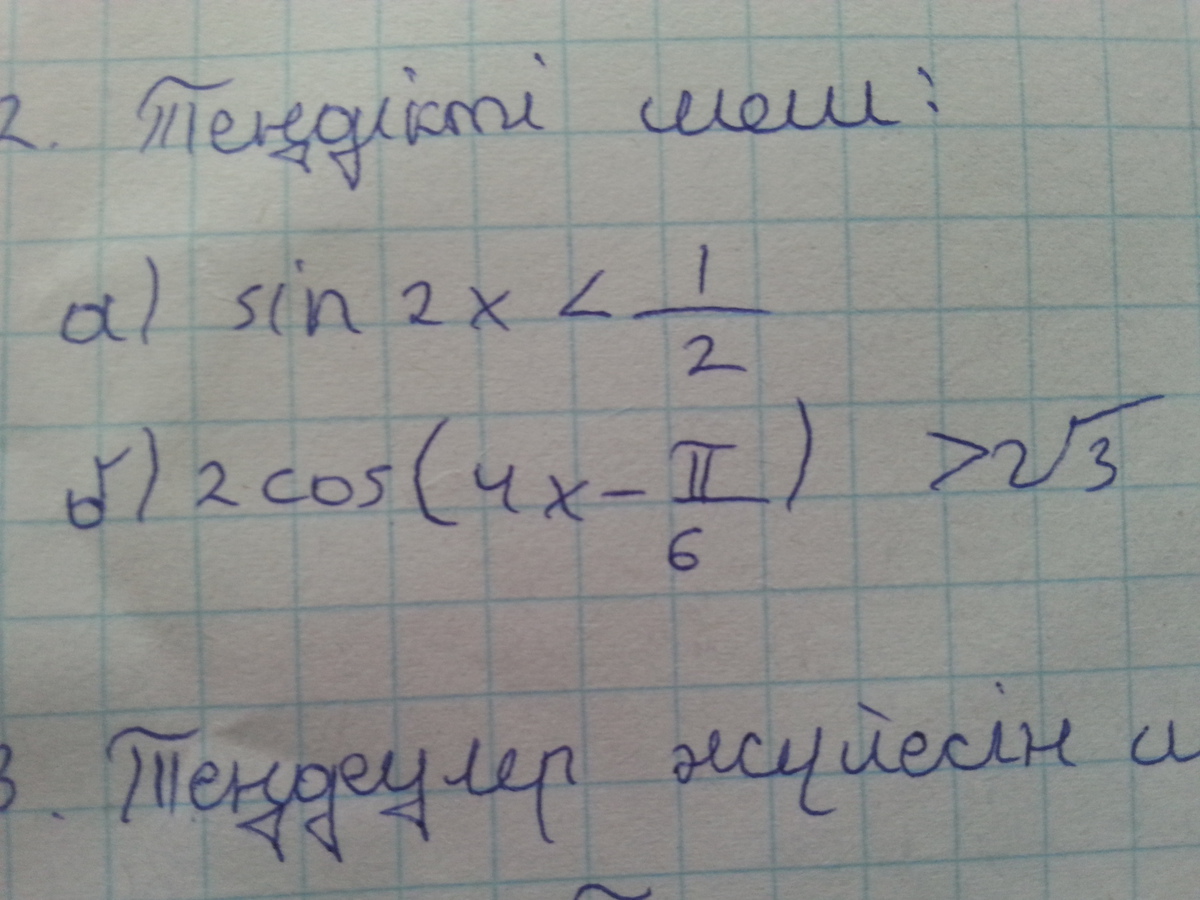
Ответы
Автор ответа:
0
1) sin2x < 1/2
-π - arcsin(1/2) + 2πn < 2x < arcsin(1/2) + 2πn, n∈Z
- π - π/6 +2πn < 2x < π/6 + 2πn, n∈Z
-7π/6 + 2πn < 2x < π/6 + 2πn, n∈Z
-7π/12 + πn < x < π/12 + πn, n∈Z
2) 2cos(4x - π/6) > √3
cos(4x - π/6) > √3/2
- arccos(√3/2) + 2πk < (4x -π/6) < arccos(√3/2) + 2πk, k∈Z
- π/6 + 2πk < (4x - π/6) < π/6 + 2πk, k∈Z
- π/6 + π/6 + 2πk < 4x < π/6 + π/6 + 2πk, k∈Z
2πk < 4x < π/3 + 2πk, k∈Z
(πk)/2 < x < π/12 + (πk)/2, k∈Z
-π - arcsin(1/2) + 2πn < 2x < arcsin(1/2) + 2πn, n∈Z
- π - π/6 +2πn < 2x < π/6 + 2πn, n∈Z
-7π/6 + 2πn < 2x < π/6 + 2πn, n∈Z
-7π/12 + πn < x < π/12 + πn, n∈Z
2) 2cos(4x - π/6) > √3
cos(4x - π/6) > √3/2
- arccos(√3/2) + 2πk < (4x -π/6) < arccos(√3/2) + 2πk, k∈Z
- π/6 + 2πk < (4x - π/6) < π/6 + 2πk, k∈Z
- π/6 + π/6 + 2πk < 4x < π/6 + π/6 + 2πk, k∈Z
2πk < 4x < π/3 + 2πk, k∈Z
(πk)/2 < x < π/12 + (πk)/2, k∈Z
Похожие вопросы
Предмет: Литература,
автор: gulder0708
Предмет: Другие предметы,
автор: erzhanovakarina
Предмет: Математика,
автор: remezovoleg2008
Предмет: Алгебра,
автор: ksv97