Предмет: Геометрия,
автор: pavviaz
В треугольнике abc ab=bc. Из вершины b выходит два отрезка к стороне ac-bk и bm. Am=kc,докозать что kb=bm и угол bkm равен углу bmk.помогите срочно!
Ответы
Автор ответа:
0
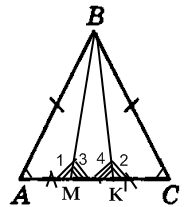
Дано: треугольник АВС; АВ=ВС; ВК, ВМ пересекают АС; АМ = КС
Доказать: КВ = ВМ; угол ВКМ = углу ВМК
Доказательство:
1.треугольник АВС - равнобедренный (АВ=ВС - дано)
треугольник ВАМ = треугольнику ВКС по первому признаку равенства треугольников (АВ=ВС - дано, АМ=КС - дано, угол ВАМ = углу ВСК), значит, все элементы треугольников равны => КВ=ВМ
2.угол 1 = углу 2 - доказано;
угол 1 + угол 3 = 180 градусов
угол 2 + угол 4 = 180 градусов
т.к. угол 1 = углу 2, угол 3= углу 4
(я знаю, доказательство 2 неточное; мысль есть - а сформулировать не получается)
Доказать: КВ = ВМ; угол ВКМ = углу ВМК
Доказательство:
1.треугольник АВС - равнобедренный (АВ=ВС - дано)
треугольник ВАМ = треугольнику ВКС по первому признаку равенства треугольников (АВ=ВС - дано, АМ=КС - дано, угол ВАМ = углу ВСК), значит, все элементы треугольников равны => КВ=ВМ
2.угол 1 = углу 2 - доказано;
угол 1 + угол 3 = 180 градусов
угол 2 + угол 4 = 180 градусов
т.к. угол 1 = углу 2, угол 3= углу 4
(я знаю, доказательство 2 неточное; мысль есть - а сформулировать не получается)
Приложения:
Автор ответа:
0
Огромное спасибо!пункт 2 очень просто,треугольник bkm равнтбедр,т.к bk=bm=>bkm=bmk
Автор ответа:
0
че-т не доперла, теперь вам спасибо =)
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Қазақ тiлi,
автор: alinafalke200
Предмет: Алгебра,
автор: metalrok2013
Предмет: Биология,
автор: diner2