Предмет: Геометрия,
автор: chaechka1
Срочно нужно. Решите, пожалуйста.
В правильной четырехугольной пирамиде плоский угол при вершине равен альфа. Найдите боковую поверхность пирамиды, если радиус круга, описного вокруг боковой грани равен R
Ответы
Автор ответа:
0
S = 4*(a²sinα)/2 = 2а²sinα, где а - длина бокового ребра, α - плоский угол при вершине
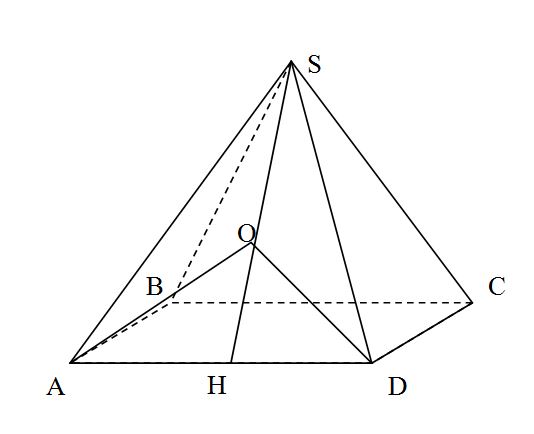
Выразим а через R. На рисунке AS = SD = a, угол ASD = α, OA = OS = OD = R (O - центр описанной около грани окружности).
уголАОС = 180-α, выразим а из ΔАОС по теореме косинусов:

Выразим а через R. На рисунке AS = SD = a, угол ASD = α, OA = OS = OD = R (O - центр описанной около грани окружности).
уголАОС = 180-α, выразим а из ΔАОС по теореме косинусов:
Приложения:
Похожие вопросы
Предмет: Химия,
автор: vadvitgorsh
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: bakytospanov1967
Предмет: Биология,
автор: Алисинька
Предмет: История,
автор: Лианочка2333