1. Площадь параллелограмма равна
96 см2, а его высоты - 6 см и 12 см. Найдите стороны параллелограмма.
2. Площадь прямоугольника со сторонами 6 см и 10 см равна площади ромба с периметром 48 см. Найдите высоту ромба.
3. Найдите площадь равнобедренного треугольника, основание которого равно 12 см, а боковая сторона - 10 см. Найдите диагонали ромба.
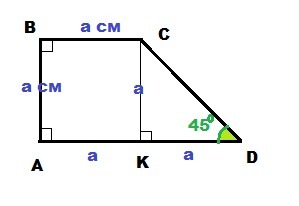
5. Меньшее основание и меньшая боковая сторона прямоугольной трапеции равны "а" см, а один из углов - 45° . Найдите площадь трапеции.
Пожалуйста, помогите решить, очень прошу!
Ответы
1. Площадь параллелограмма вычисляется по формуле
S = ah, где h - высота, проведенная к стороне a.
S = ah₁; 96 = a*6; a = 96/6 = 16 см
S = bh₂; 96 = b*12; b = 96/12 = 8 см
У параллелограмма противоположные стороны попарно параллельны и равны.
Ответ: две стороны по 16 см, две стороны по 8 см
=============================
2. Площадь прямоугольника
S = ab = 6*10 = 60 см²
У ромба все стороны равны, а так как периметр - это сумма четырех равных сторон, то сторона ромба равна
c = 48 / 4 = 12 см
Ромб - это параллелограмм с равными сторонами. Площадь
S = ch, где h - высота.
60 = 12*h; h = 60/12 = 5 см
Ответ: высота ромба равна 5 см
============================
3. Боковые стороны равнобедренного треугольника равны по 10 см, основание 12 см.
Полупериметр треугольника p = (10+10+12)/2 = 16 см
Формула Герона
Ответ: площадь треугольника 48 см²
Фраза "найдите диагонали ромба", видимо, относится к удаленному 4 заданию.
============================
5. Трапеция ABCD - прямоугольная, ∠A=∠B=90°; ∠D = 45°
BC║AD - основания, BC = AB = a см (см. рисунок)
Боковая сторона AB является высотой трапеции, так как перпендикулярна основаниям.
Опустить высоту CK = AB = a
ABCK - прямоугольник, AK = BC = a
ΔCDK - прямоугольный, ∠K = 90°; ∠D = 45° ⇒
∠KCD = 90° - 45° = 45° ⇒
ΔCDK - равнобедренный прямоугольный, KD = CK = a
AD = AK + KD = a + a = 2a
Площадь трапеции
Ответ: площадь трапеции 1,5a² см²