Предмет: Алгебра,
автор: grenlandialol
Как найти такую площадь? Применяя интегралы? Помогите пожалуйста
Приложения:

Ответы
Автор ответа:
0
Рисунок во вложении.

Сведём данный интеграл к повторному.

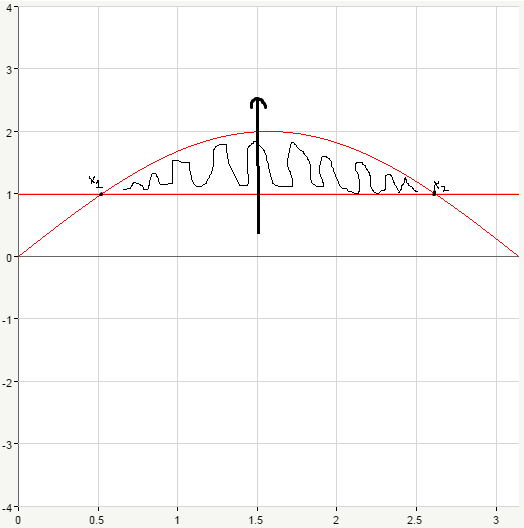
Сначала нам нужно узнать в какие пределах изменяется х, для этого найдём точки пересечения графиков(на рисунке это точки х1 и х2):
2sinx=1
sinx=1/2
x=(-1)^n * arcsin(1/2) + π*n, n∈Z
Из этого уравнения выбираем точки которые входят в промежуток от [0;pi]:
n=0 => x=arcsin(1/2)=π/6 (x1 на рисунке)
n=1=> x=-arcsin(1/2)+π=-π/6+π=5π/6 (х2 на рисунке)
Это и буду наши пределы интегрирования по х.
Теперь нам нужно узнать в какие пределах у нас изменяется y, для этого на рисунке проведём прямую проходящую через нашу фигуру и параллельную оси y. Теперь смотрим через какую линию она входит, и через какую выходит. Входит наша прямая через линию х=1, а выходит через линию y=2sinx, значит у изменяется от 1 до 2sinx. Ну вот и всё, нашли пределы интегрирования, подставляем и считаем:

Сведём данный интеграл к повторному.
Сначала нам нужно узнать в какие пределах изменяется х, для этого найдём точки пересечения графиков(на рисунке это точки х1 и х2):
2sinx=1
sinx=1/2
x=(-1)^n * arcsin(1/2) + π*n, n∈Z
Из этого уравнения выбираем точки которые входят в промежуток от [0;pi]:
n=0 => x=arcsin(1/2)=π/6 (x1 на рисунке)
n=1=> x=-arcsin(1/2)+π=-π/6+π=5π/6 (х2 на рисунке)
Это и буду наши пределы интегрирования по х.
Теперь нам нужно узнать в какие пределах у нас изменяется y, для этого на рисунке проведём прямую проходящую через нашу фигуру и параллельную оси y. Теперь смотрим через какую линию она входит, и через какую выходит. Входит наша прямая через линию х=1, а выходит через линию y=2sinx, значит у изменяется от 1 до 2sinx. Ну вот и всё, нашли пределы интегрирования, подставляем и считаем:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: xhtxydcyfyf
Предмет: Английский язык,
автор: yanattt0
Предмет: Английский язык,
автор: kristinapolinina2019
Предмет: Информатика,
автор: dugy3d
Предмет: Геометрия,
автор: danilus907