Предмет: Геометрия,
автор: ddi
тема замечательные точки треугольника доказать что любая точка биссектрисы угла равноудалена от его сторон теорема 19
Ответы
Автор ответа:
0
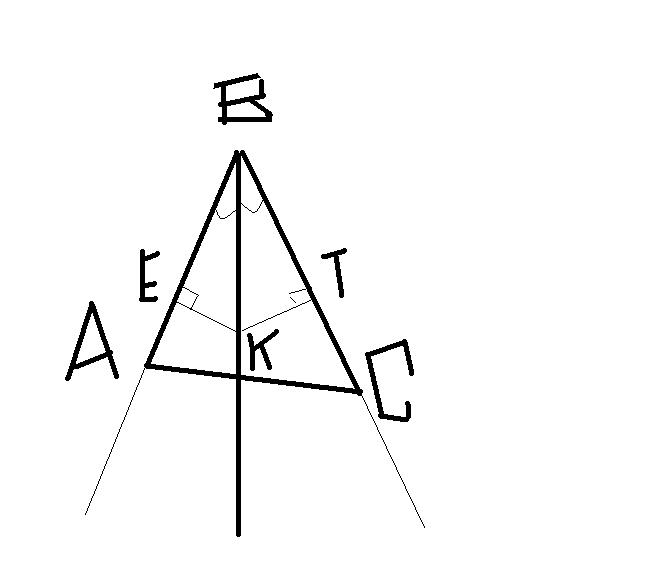
Пусть АВС - данный треугольник. ВК - биссектрисса угла В, пусть Р -произвольная точка на биссектриссе ВК. Опустим перпендикуляры на лучи ВА и ВС. Пусть Е и Т - точки оснований. По определению ЕР и ТР - расстояния от точки Р до сторон ВА и ВС.
Докажем, что ВА=ВС (т.е. требуемое утверждение)
Треугольники РВЕ и РВТ равные, как прямоугольные треугольники с одинаковыми гипотенузами РВ=РВ и равными острыми углами (угол РВЕ=угол РВТ - из определения биссектриссы). Из равенства треугольников следует равенство их сторон
ВА=ВС.
Таким образом
любая точка биссектрисы угла равноудалена от его сторон. Доказано
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Triss123466
Предмет: Информатика,
автор: KADYRZHANAR
Предмет: Алгебра,
автор: bayastanmatraimov3
Предмет: Математика,
автор: Умни
Предмет: Физика,
автор: ViktoriaDV