Предмет: Геометрия,
автор: Аноним
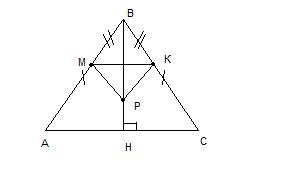
На высоте равнобедренного треугольника АВС, проведенной к основанию АС, взята точка Р, а на сторонах АВ и ВС – точки М и К соответственно (точки М,Р и
Невероятная история о сигналах для торговли бинарными опционами (24hoptions)
К не лежат на одной прямой). Известно, что ВМ = ВК. Докажите, что: а) углы ВМР и ВКР равны; б) углы КМР и РКМ равны. Помогите пожалуйста!
Ответы
Автор ответа:
0
а). Рассмотрим треугольники ВМР и ВКР. Они равны по двум сторонам и углу между ними:
- ВМ=ВК по условию;
- ВР - общая сторона;
- углы МВР и КВР равны, т.к. высота ВН равнобедренного треугольника АВС, проведенная к его основанию АС является также и биссектрисой.
В равных треугольниках ВМР и ВКР равны соответственные углы ВМР и ВКР.
б). Рассмотрим треугольник МРК. Здесь РМ=РК как соответственные стороны равных треугольников ВМР и ВКР. Значит МРК - равнобедренный треугольник, следовательно, углы КМР и МКР при его основании МК равны.
- ВМ=ВК по условию;
- ВР - общая сторона;
- углы МВР и КВР равны, т.к. высота ВН равнобедренного треугольника АВС, проведенная к его основанию АС является также и биссектрисой.
В равных треугольниках ВМР и ВКР равны соответственные углы ВМР и ВКР.
б). Рассмотрим треугольник МРК. Здесь РМ=РК как соответственные стороны равных треугольников ВМР и ВКР. Значит МРК - равнобедренный треугольник, следовательно, углы КМР и МКР при его основании МК равны.
Приложения:
Похожие вопросы
Предмет: Физика,
автор: sanyaaleksandr2020ru
Предмет: Немецкий язык,
автор: morghalik
Предмет: Математика,
автор: sofikol09
Предмет: Математика,
автор: denchikvedernikov