Предмет: Геометрия,
автор: Virc
Решите все задачи с ПОЛНЫМ РЕШЕНИЕМ
С рисунками,с пояснениями,с ссылками на теоремы
260 БАЛЛОВ
Приложения:

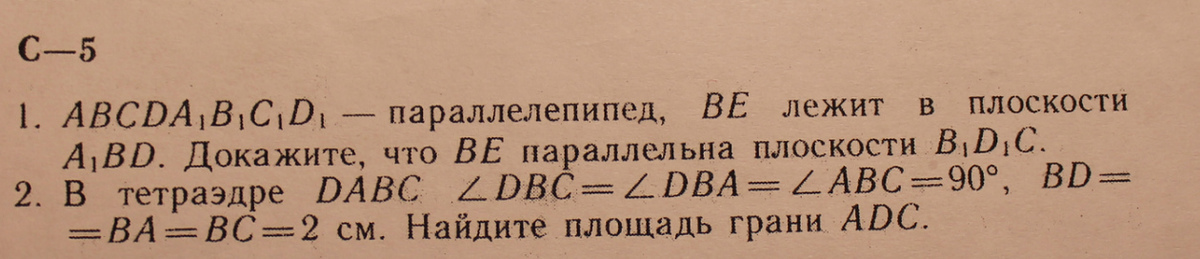
Ответы
Автор ответа:
0
1. По обратной теореме Фалеса , если прямые, пересекающие две другие прямые, отсекают на обеих из них пропорциональные между собой отрезки, то такие прямые параллельны. Значит прямая EF||BC.
Прямая EF принадлежит плоскости α. Значит ВС||α.
2. По свойству параллельных прямых: если одна из пары параллельных прямых параллельна третьей прямой, то вторая прямая тоже параллельна третьей. Таким образом, a||c b||a, из этого следует что b||c.
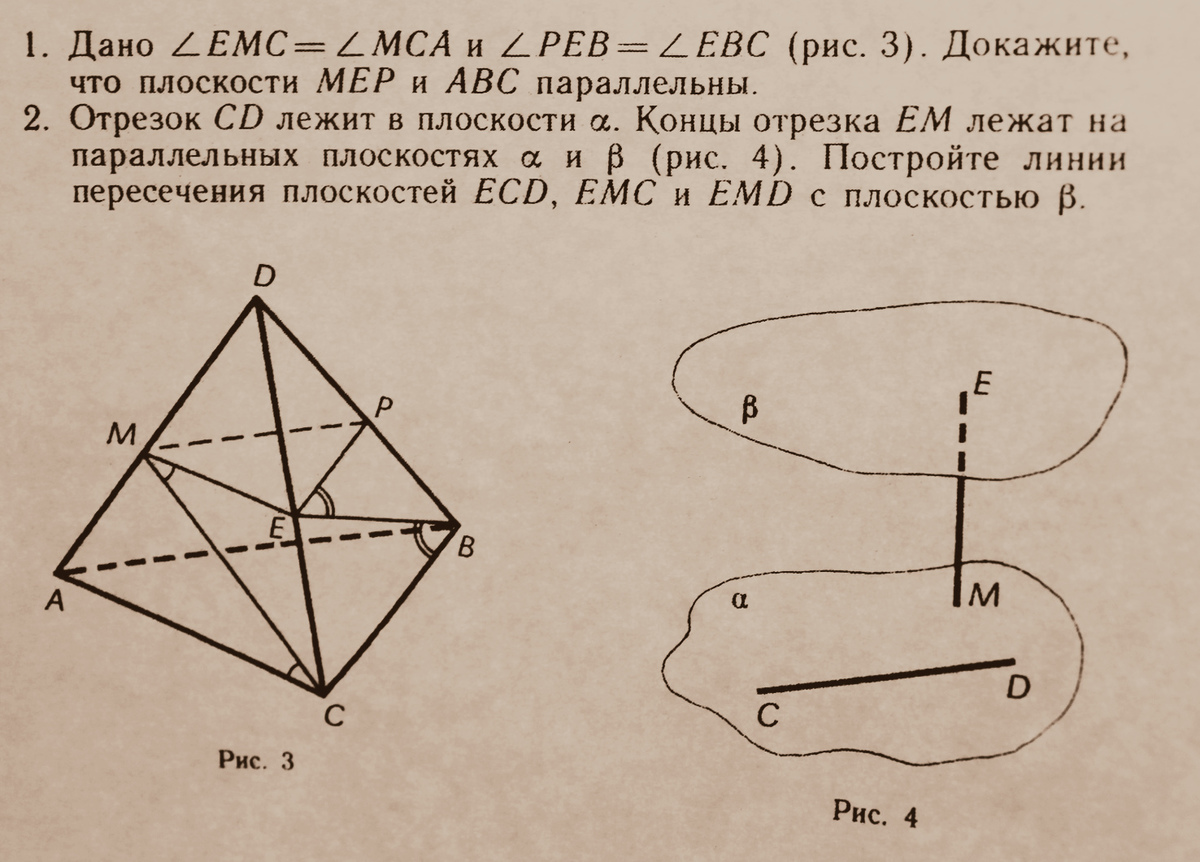
1. ME||AC так как накрест лежащие углы равны.
PE||BC так как накрест лежащие углы равны.
Две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости. Значит плоскости МЕР и АВС параллельны.
2. Чтобы построить линии пересечения надо из точки Е провести прямую параллельную:
Для ECD - CD
Для EMC - MC
Для EMD - MD
1. BD||B1D1
D1C||A1B
Значит плоскость A1BD|| плоскости B1D1C, и значит прямая ВЕ принадлежащая плоскости A1BD параллельная плоскости B1D1C
2. ADC равносторонний треугольник со стороной

Прямая EF принадлежит плоскости α. Значит ВС||α.
2. По свойству параллельных прямых: если одна из пары параллельных прямых параллельна третьей прямой, то вторая прямая тоже параллельна третьей. Таким образом, a||c b||a, из этого следует что b||c.
1. ME||AC так как накрест лежащие углы равны.
PE||BC так как накрест лежащие углы равны.
Две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости. Значит плоскости МЕР и АВС параллельны.
2. Чтобы построить линии пересечения надо из точки Е провести прямую параллельную:
Для ECD - CD
Для EMC - MC
Для EMD - MD
1. BD||B1D1
D1C||A1B
Значит плоскость A1BD|| плоскости B1D1C, и значит прямая ВЕ принадлежащая плоскости A1BD параллельная плоскости B1D1C
2. ADC равносторонний треугольник со стороной
Похожие вопросы
Предмет: Русский язык,
автор: golubevaaaluna
Предмет: Английский язык,
автор: aimonalee
Предмет: Физика,
автор: Lokamoka
Предмет: Химия,
автор: Lena0015
Предмет: Алгебра,
автор: 69Котуха69