Question

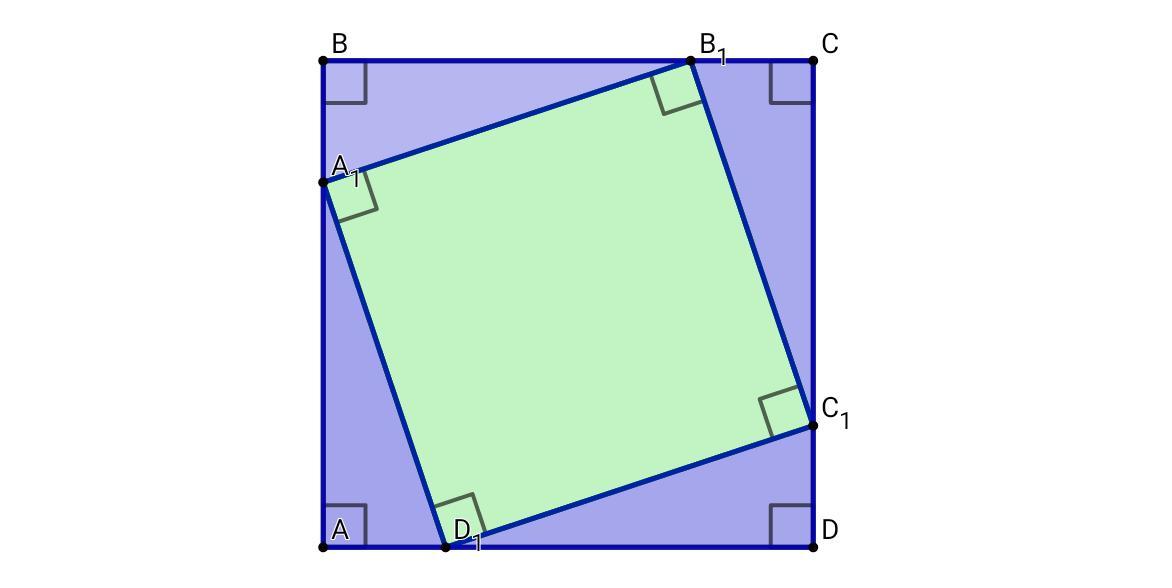
Дан квадрат ABCD. На каждой его стороне отложены равные отрезки AA1=CC1=DD1. Докажите, что четырехугольник A1B1C1D1 тоже являются квадратом.

Answer 1

,Так как точки отложены на одинаковом расстоянии, то у полученной фигуры стороны параллельны. Далее рассматривать через  равенство прямоугольных треугольников (А1ВВ!, В1СС1, С1ДД1 и Д1ДА1). Их гипотенузы равны, углы А1,В1, С1 иД1 по 90град. Полученная фигура -квадрат

Answer 2

см.рисунок----------------------------------------------

отметь как лучшее, пожайлуста)))

Answer 3

A₁B = AB - AA₁ , B₁C = BC - BB₁ , C₁D = CD - CC₁ , AD₁ = AD - DD₁

Но АВ = ВС = CD = AD и AA₁ = BB₁ = CC₁ = DD₁ ⇒ А₁В = В₁С = С₁D = AD₁

Таким образом, ΔА₁ВВ₁ = ΔВ₁СС₁ = ΔС₁DD₁ = ΔA₁AD₁ по двум катетам ⇒ ∠А₁В₁В = ∠АА₁D₁ , ∠BA₁B₁ + ∠A₁В₁B = 90° = ∠BA₁B₁ + ∠AA₁D₁

∠B₁A₁D₁ = 180° - (∠BA₁B₁ + ∠AA₁D₁) = 180° - 90° = 90°

А₁В₁ = В₁С₁ = C₁D₁ = A₁D₁ как гипотенузы равных прям-ых треугольников, А₁B₁C₁D₁ - ромб с прямым углом ⇒ A₁B₁C₁D₁ - квадрат, ч.т.д.