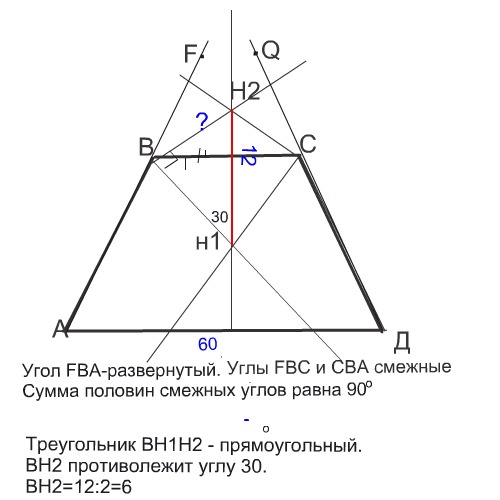
В равнобедренной трапеции АВСД биссектрисы углов АВС и ВСД пересекаются в точке Н1. На прямых АВ и СД взяты точки F и Q, так что В лежит между А и F, а С - между D и Q. Биссектрисы углов FBC и BCQ пересекаются в точке Н2. Длина отрезка Н1Н2=12 см. Найдите длину ВН2, если угол ВН1С=60о.
Ответы
Для решения задачи нужно сделать рисунок.
Углы при основаниях равнобедренной трапеции равны, а биссектрисы равных углов В и С делят их на равные половины.
В треугольниках ВН₁С и ВН₂С с общим основанием ВС углы при основании равны, следовательно, они равнобедренные.
Углы Н₂ВН₁ и Н₂СН₁ состоят из половин смежных углов и поэтому равны 90°
Катеты прямоугольных треугольников Н₂ВН₁ и Н₂СН₁ равны, гипотенуза общая - треугольники равны, и их острые углы при гипотенузе Н₂Н₁ равны.
Поэтому Н₁Н₂ - биссектриса угла ВН₁С и делит его на два по 30°.
Катет ВН₂ противолежит углу 30° и по свойству такого катета равен половине гипотенузы Н₁Н₂ ( или ВН₂=Н₁Н₂•sin30º)
Отрезок ВН₂=12:2=6см