Предмет: Геометрия,
автор: rada20102
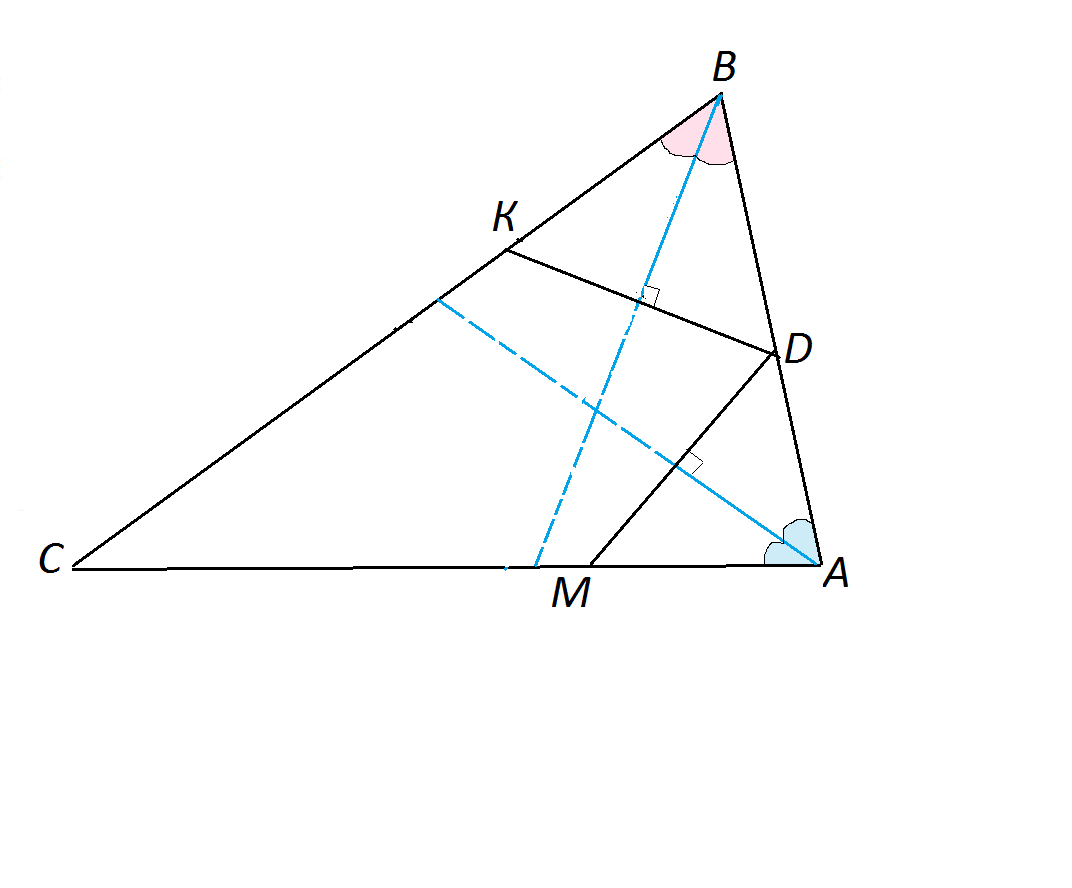
через середину D стороны AB треугольника ABC проведены прямые перпендикулярные биссектрисам углов ABC и BAC .Эти прямые пересекают стороны AC и BC в точках M и K соответственно . Докажите , что AM=BK
Ответы
Автор ответа:
0
Рассмотри треугольники ВКD и АМD.
В них основания перпендикулярны биссектрисам, а биссектрисы перпендикулярны по условию основаниям -
в Δ ВКD основанию КD,
в Δ АМD основанию МD.
Следовательно, биссектрисы являются в этих треугольниках и высотами. Треугольник, в котором биссектриса является одновременно высотой - равнобедренный.
Треугольники ВКD и АМD равнобедренные.
По условию ВD=АD.
Следовательно, боковые стороны этих треугольников равны, отсюда ВК=АМ.
В них основания перпендикулярны биссектрисам, а биссектрисы перпендикулярны по условию основаниям -
в Δ ВКD основанию КD,
в Δ АМD основанию МD.
Следовательно, биссектрисы являются в этих треугольниках и высотами. Треугольник, в котором биссектриса является одновременно высотой - равнобедренный.
Треугольники ВКD и АМD равнобедренные.
По условию ВD=АD.
Следовательно, боковые стороны этих треугольников равны, отсюда ВК=АМ.
Приложения:
Автор ответа:
0
Спасибо большое
Похожие вопросы
Предмет: Химия,
автор: rafa20050807
Предмет: Оʻzbek tili,
автор: Unknowncat
Предмет: История,
автор: Аноним
Предмет: Математика,
автор: Улька2001ТыСупер
Предмет: Биология,
автор: kykyskin89