Предмет: Алгебра,
автор: NathanYoung
Помогите решить задание, с подробным объяснением! Пожалуйста!
Приложения:
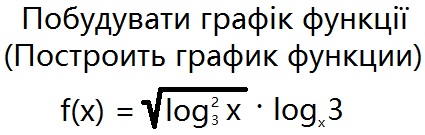
Ответы
Автор ответа:
0
Найдём область допустимых значений (ОДЗ):
D(y):x>0; x≠1
Преобразуем функцию:

Когда ⇒
⇒
Когда ⇒
⇒
Если что:

Рисуем график(не забываем про ОДЗ(x>0;x≠1)):
D(y):x>0; x≠1
Преобразуем функцию:
Когда
Когда
Если что:
Рисуем график(не забываем про ОДЗ(x>0;x≠1)):
Приложения:

Автор ответа:
0
а можно ещё и построенный график?)
Автор ответа:
0
так с самого низу вложение.
Автор ответа:
0
простите, не увидел. у меня бывает такое :D
Автор ответа:
0
График требует уточнения
Автор ответа:
0
f(x)=/log(3)x/*1/log(3)x=(/log(3)x/)/log(3)x
ОДЗ x>0 U x≠1⇒x∈(0;1) U (1;∞)
1)x∈(0;1)
f(x)=-log(3)x/log(3)x=-1
2)x∈(1;∞)
f(x)=log(3)x/log(3)x=1
График во вложении .Не забудь "выколоть" точки
ОДЗ x>0 U x≠1⇒x∈(0;1) U (1;∞)
1)x∈(0;1)
f(x)=-log(3)x/log(3)x=-1
2)x∈(1;∞)
f(x)=log(3)x/log(3)x=1
График во вложении .Не забудь "выколоть" точки
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Физика,
автор: LinMakne4ka
Предмет: Биология,
автор: marvin18
Предмет: Алгебра,
автор: nadywa